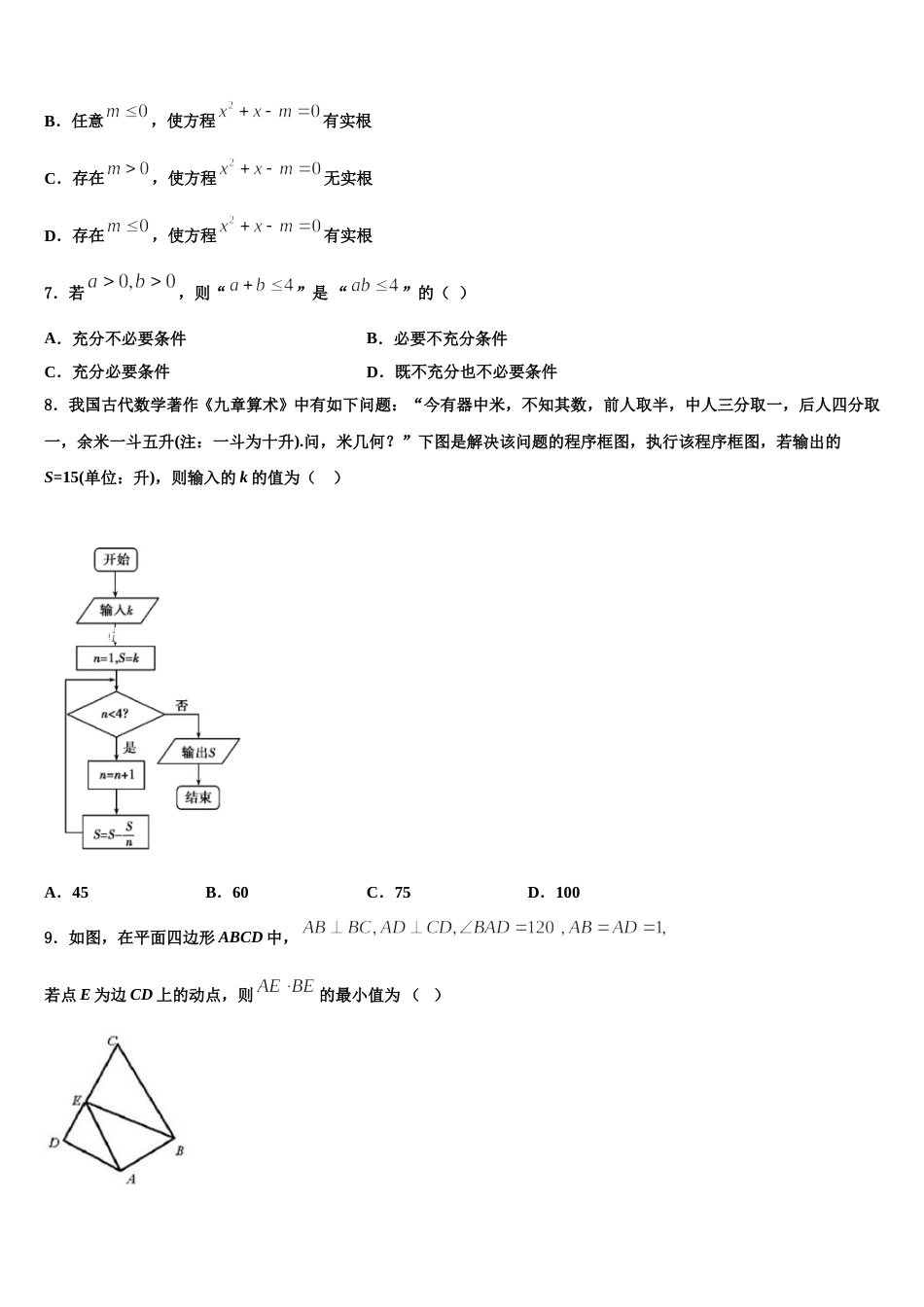
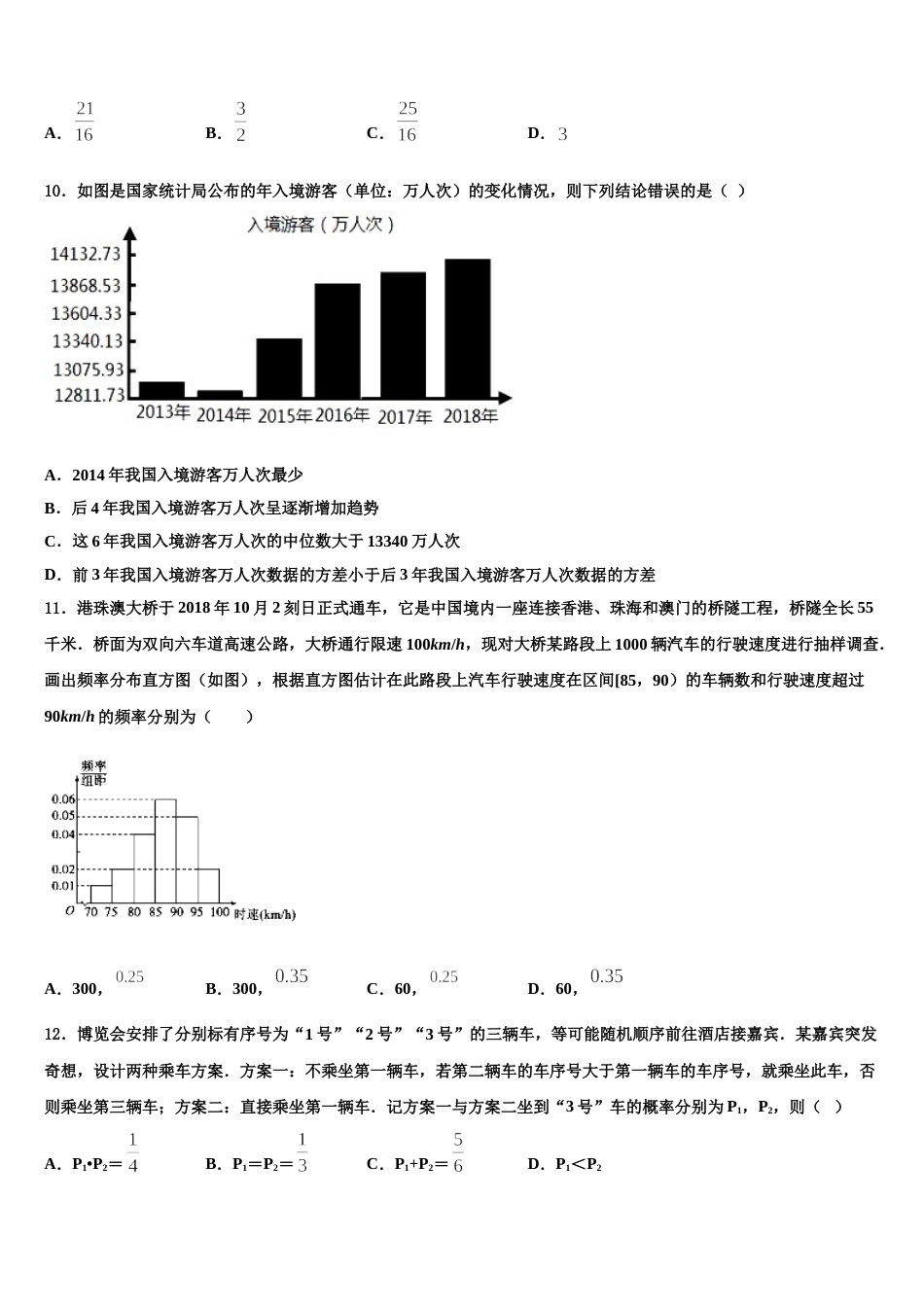
四川成都青羊区外国语学校 2023-2024 学年高三一诊考试数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知在中,角的对边分别为,若函数存在极值,则角的取值范围是( )A.B.C.D.2.公差不为零的等差数列{an}中,a1+a2+a5=13,且 a1、a2、a5成等比数列,则数列{an}的公差等于( )A.1B.2C.3D.43.已知函数,若关于的方程恰好有 3 个不相等的实数根,则实数的取值范围为( )A.B.C.D.4.如果直线与圆相交,则点与圆 C 的位置关系是( )A.点 M 在圆 C 上B.点 M 在圆 C 外C.点 M 在圆 C 内D.上述三种情况都有可能5.设是定义域为的偶函数,且在单调递增,,则( )A.B.C.D.6.设,命题“存在,使方程有实根”的否定是( )A.任意,使方程无实根B.任意,使方程有实根C.存在,使方程无实根D.存在,使方程有实根7.若,则“”是 “”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件8.我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升(注:一斗为十升).问,米几何?”下图是解决该问题的程序框图,执行该程序框图,若输出的S=15(单位:升),则输入的 k 的值为( ) A.45B.60C.75D.1009.如图,在平面四边形 ABCD 中,若点 E 为边 CD 上的动点,则的最小值为 ( )A.B.C.D.10.如图是国家统计局公布的年入境游客(单位:万人次)的变化情况,则下列结论错误的是( ) A.2014 年我国入境游客万人次最少B.后 4 年我国入境游客万人次呈逐渐增加趋势C.这 6 年我国入境游客万人次的中位数大于 13340 万人次D.前 3 年我国入境游客万人次数据的方差小于后 3 年我国入境游客万人次数据的方差11.港珠澳大桥于 2018 年 10 月 2 刻日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长 55千米.桥面为双向六车道高速公路,大桥通行限速 100km/h,现对大桥某路段上 1000 辆汽车的行驶速度进行抽样调查.画出频率分布直方图(如图),根据直方图估计在此路段上汽车行驶速度在区间[85,90)的车辆数和行驶速度超过90km/h 的频率分别为( )A.300,B.300,C.60,D.60,12.博览会安排了分别标有序号为“1 号”“2 号”“3 号”的三辆车,等可能随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“3 号”车的概率分别为 P1,P2,则( )A.P1•P2=B.P1=P2=C.P1+P2=D.P1<P2二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知 x,y>0,且,则 x+y 的最小值为_____.14.的展开式中的系数为____.15.过点,且圆心在直线上的圆的半径为__________.16.已知以 x±2y =0 为渐近线的双曲线经过点,则该双曲线的标准方程为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知曲线的参数方程为为参数 , 曲线的参数方程为为参数).(1)求与的普通方程;(2)若与相交于,两点,且,求的值.18.(12 分)已知函数的定义域为,且满足,当时,有,且.(1)求不等式的解集;(2)对任意,恒成立,求实数的取值范围.19.(12 分)已知函数,.(1)当时,判断是否是函数的极值点,并说明理由;(2)当时,不等式恒成立,求整数的最小值.20.(12 分)如图,平面四边形为直角梯形,,,,将绕着翻折到.(1)为上一点,且,当平面时,求实数的值;(2)当平面与平面所成的锐二面角大小为时,求与平面所...