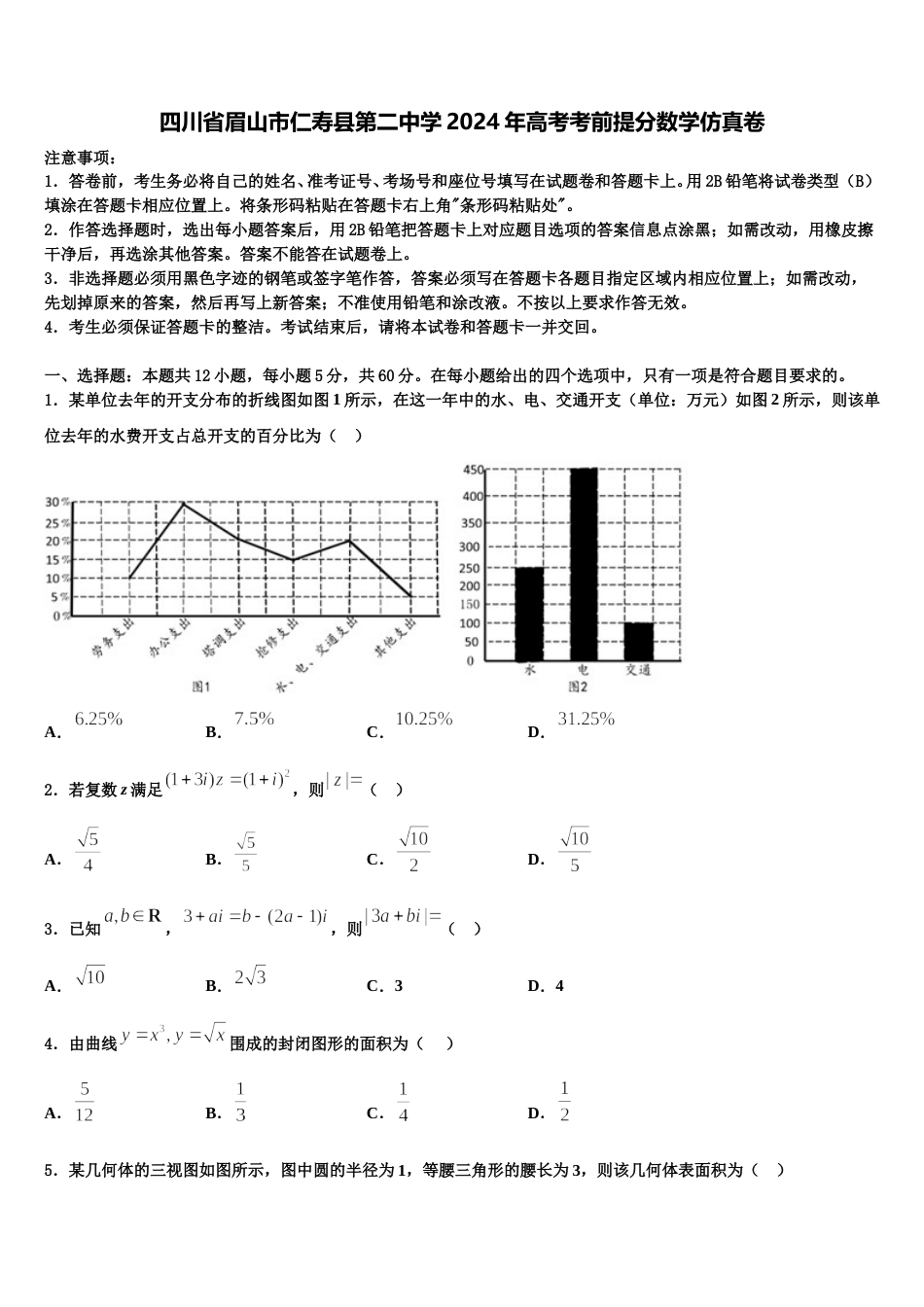
四川省眉山市仁寿县第二中学 2024 年高考考前提分数学仿真卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用 2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某单位去年的开支分布的折线图如图 1 所示,在这一年中的水、电、交通开支(单位:万元)如图 2 所示,则该单位去年的水费开支占总开支的百分比为( )A.B.C.D.2.若复数 z 满足,则( )A.B.C.D.3.已知,,则( )A.B.C.3D.44.由曲线围成的封闭图形的面积为( )A.B.C.D.5.某几何体的三视图如图所示,图中圆的半径为 1,等腰三角形的腰长为 3,则该几何体表面积为( )A.B.C.D.6.若双曲线的离心率为,则双曲线的焦距为( )A.B.C.6D.87.已知函数且的图象恒过定点,则函数图象以点为对称中心的充要条件是( )A.B.C.D.8.已知复数满足,且,则( )A.3B.C.D.9.下图是来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形的斜边、直角边,已知以直角边为直径的半圆的面积之比为,记,则( )A.B.C.1D.10.抛物线的准线方程是,则实数( )A.B.C.D.11.抛物线的焦点为 F,点为该抛物线上的动点,若点,则的最小值为( )A.B.C.D.12.已知点 P 在椭圆 τ:=1(a>b>0)上,点 P 在第一象限,点 P 关于原点 O 的对称点为 A,点 P 关于 x 轴的对称点为 Q,设,直线 AD 与椭圆 τ 的另一个交点为 B,若 PA⊥PB,则椭圆 τ 的离心率 e=( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.设变量,满足约束条件,则目标函数的最小值为______.14.如图,在中,,,,点在边上,且,将射线绕着逆时针方向旋转,并在所得射线上取一点,使得,连接,则的面积为__________.15.某高中共有 1800 人,其中高一、高二、高三年级的人数依次成等差数列,现用分层抽样的方法从中抽取 60 人,那么高二年级被抽取的人数为________.16.如图,两个同心圆的半径分别为和,为大圆的一条 直径,过点作小圆的切线交大圆于另一点,切点为,点为劣弧上的任一点(不包括 两点),则的最大值是__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数.(1)时,求不等式解集;(2)若的解集包含于,求 a 的取值范围.18.(12 分)已知.(1)求不等式的解集;(2)记的最小值为,且正实数满足.证明:.19.(12 分)贫困人口全面脱贫是全面建成小康社会的标志性指标.党的十九届四中全会提出“坚决打赢脱贫攻坚战,建立解决相对贫困的长效机制”对当前和下一个阶段的扶贫工作进行了前瞻性的部署,即 2020 年要通过精准扶贫全面消除绝对贫困,实现全面建成小康社会的奋斗目标.为了响应党的号召,某市对口某贫困乡镇开展扶贫工作.对某种农产品加工生产销售进行指导,经调查知,在一个销售季度内,每售出一吨该产品获利 5 万元,未售出的商品,每吨亏损 2 万元.经统计,两市场以往 100 个销售周期该产品的市场需求量的频数分布如下表:市场:需求量(吨)90100110频数205030市场:需求量(吨)90100110频数106030把市场需求量的频率视为需求量的概率,设该厂在下个销售周期内生产吨该产品,在、两市场同时销售,以(单位:吨)表示下一个销售周期两市场的需求量...