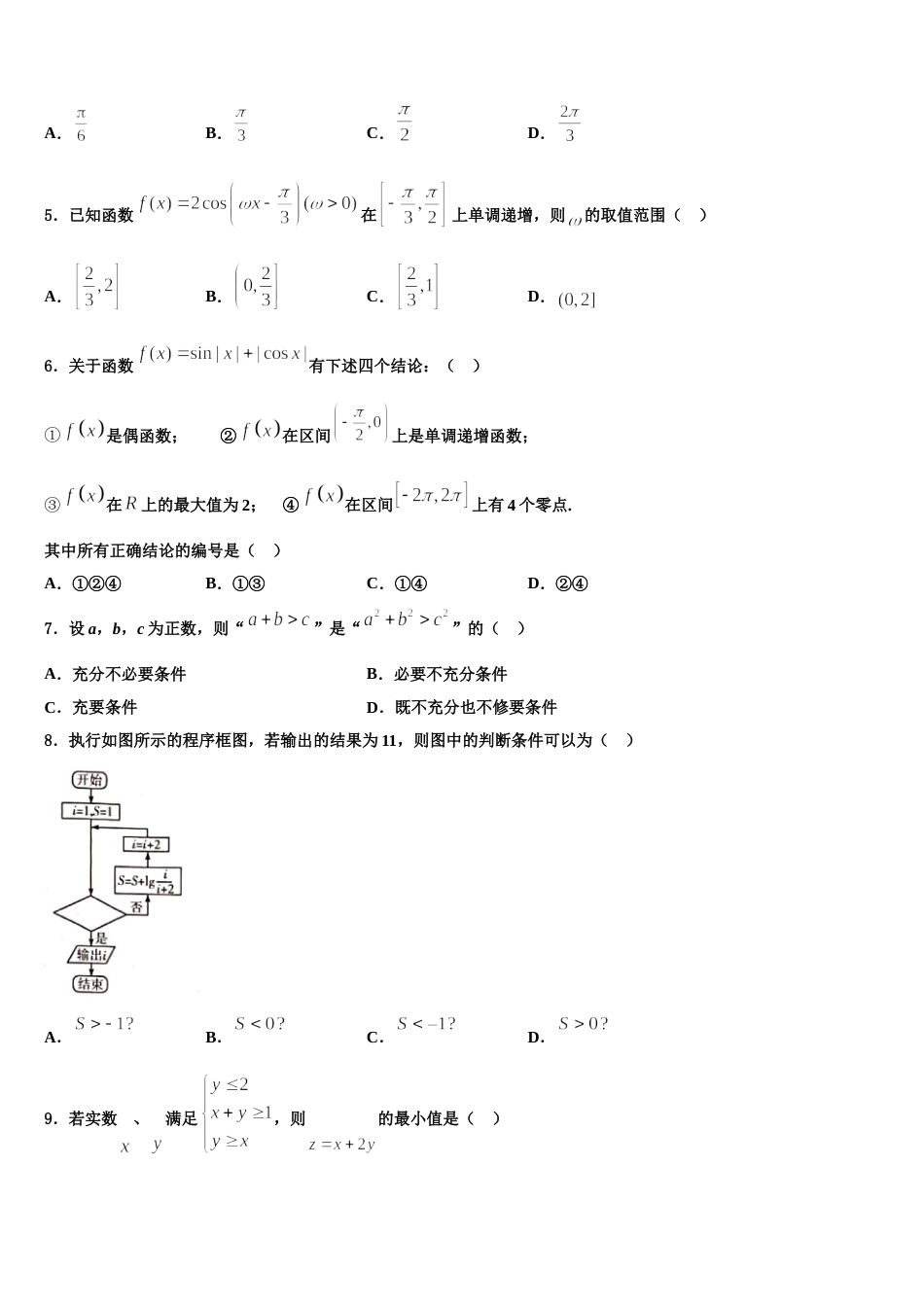
天津市武清区 2024 届高考数学五模试卷注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若双曲线的渐近线与圆相切,则双曲线的离心率为( )A.2B.C.D.2.阿波罗尼斯(约公元前 262~190 年)证明过这样的命题:平面内到两定点距离之比为常数的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点,间的距离为 2,动点与,的距离之比为,当,,不共线时,的面积的最大值是( )A.B.C.D.3.设 P={y |y=-x2+1,x∈R},Q={y |y=2x,x∈R},则A.P QB.Q PC.QD.Q 4.点是单位圆上不同的三点,线段与线段交于圆内一点 M,若,则的最小值为( ) A.B.C.D.5.已知函数在上单调递增,则的取值范围( )A.B.C.D.6.关于函数有下述四个结论:( )①是偶函数; ②在区间上是单调递增函数;③在上的最大值为 2; ④在区间上有 4 个零点.其中所有正确结论的编号是( )A.①②④B.①③C.①④D.②④7.设 a,b,c 为正数,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不修要条件8.执行如图所示的程序框图,若输出的结果为 11,则图中的判断条件可以为( )A.B.C.D.9.若实数、满足,则的最小值是( )A.B.C.D.10.已知三棱锥的体积为 2,是边长为 2 的等边三角形,且三棱锥的外接球的球心恰好是中点,则球的表面积为( )A.B.C.D.11.已知集合,,则( )A.B.C.D.12.若,则的值为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知是等比数列,若,,且∥,则______.14.在四棱锥中,是边长为的正三角形,为矩形,,.若四棱锥的顶点均在球的球面上,则球的表面积为_____.15.的展开式中的常数项为__________.16.抛物线的焦点到准线 的距离为 .三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知件次品和件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出件次品或者检测出件正品时检测结束.(1)求第一次检测出的是次品且第二次检测出的是正品的概率;(2)已知每检测一件产品需要费用元,设表示直到检测出件次品或者检测出件正品时所需要的检测费用(单位:元),求的分布列.18.(12 分)已知椭圆的左、右焦点分别为直线 垂直于轴,垂足为,与抛物线交于不同的两点,且过的直线与椭圆交于两点,设且 .(1)求点的坐标;(2)求的取值范围.19.(12 分)设前项积为的数列,(为常数),且是等差数列.(I)求的值及数列的通项公式;(Ⅱ)设是数列的前项和,且,求的最小值.20.(12 分)设函数.(1)当时,求不等式的解集;(2)当时,求实数的取值范围.21.(12 分)在平面直角坐标系中,曲线的参数方程为(为参数),以原点为极点,轴的非负半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)求曲线的极坐标方程以及曲线的直角坐标方程;(2)若直线与曲线、曲线在第一象限交于两点,且,点的坐标为,求的面积.22.(10 分)若,且(1)求的最小值;(2)是否存在,使得?并说明理由.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】利用圆心到渐近线的距离等于半径即可建立间的关系.【详解】由已知,双曲线的渐近线方程为,故圆心到渐近线的距...