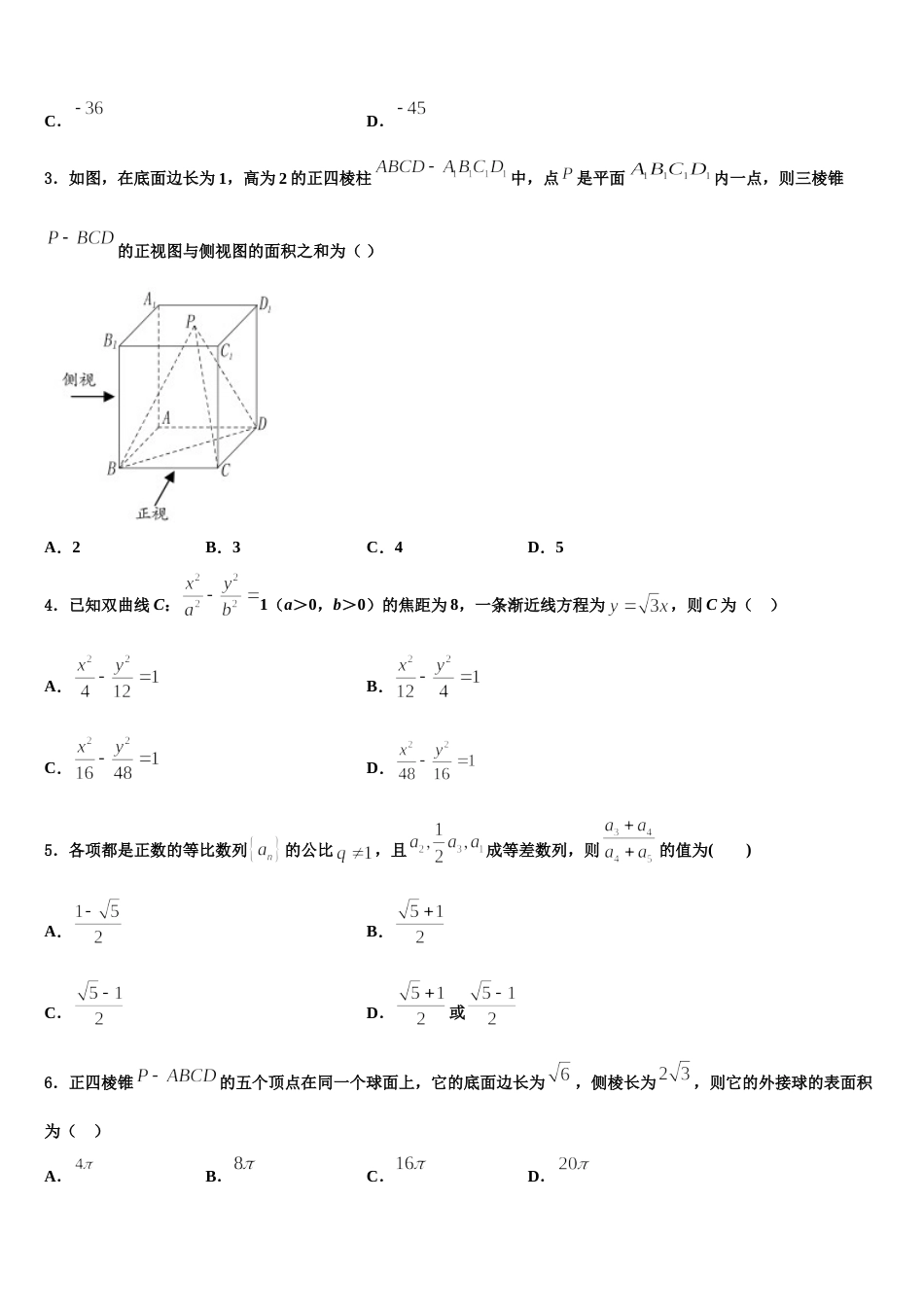
宁夏省银川市 2024 届高三六校第一次联考数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图,90 后从事互联网行业岗位分布条形图,则下列结论中不正确的是( )注:90 后指 1990 年及以后出生,80 后指 1980-1989 年之间出生,80 前指 1979 年及以前出生.A.互联网行业从业人员中 90 后占一半以上B.互联网行业中从事技术岗位的人数超过总人数的C.互联网行业中从事运营岗位的人数 90 后比 80 前多D.互联网行业中从事技术岗位的人数 90 后比 80 后多2.执行如下的程序框图,则输出的是( )A.B.C.D.3.如图,在底面边长为 1,高为 2 的正四棱柱中,点是平面内一点,则三棱锥的正视图与侧视图的面积之和为( )A.2B.3C.4D.54.已知双曲线 C:1(a>0,b>0)的焦距为 8,一条渐近线方程为,则 C 为( )A.B.C.D.5.各项都是正数的等比数列的公比,且成等差数列,则的值为( )A.B.C.D.或6.正四棱锥的五个顶点在同一个球面上,它的底面边长为,侧棱长为,则它的外接球的表面积为( )A.B.C.D.7.关于圆周率 π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计的值:先请全校名同学每人随机写下一个都小于 的正实数对;再统计两数能与 构成钝角三角形三边的数对的个数;最后再根据统计数估计的值,那么可以估计的值约为( )A.B.C.D.8.设,则复数的模等于( )A.B.C.D.9.在边长为的菱形中,,沿对角线折成二面角为的四面体(如图),则此四面体的外接球表面积为( )A.B.C.D.10.袋中装有标号为 1,2,3,4,5,6 且大小相同的 6 个小球,从袋子中一次性摸出两个球,记下号码并放回,如果两个号码的和是 3 的倍数,则获奖,若有 5 人参与摸球,则恰好 2 人获奖的概率是( )A.B.C.D.11.某学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为的样本,其频率分布直方图如图所示,其中支出在(单位:元)的同学有 34 人,则的值为( )A.100B.1000C.90D.9012.已知函数,若关于的方程有 4 个不同的实数根,则实数的取值范围为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若、满足约束条件,则的最小值为______.14.从编号为 ,,,的张卡片中随机抽取一张,放回后再随机抽取一张,则第二次抽得的卡片上的数字能被第一次抽得的卡片上数字整除的概率为_____________.15.如图所示,平面 BCC1B1⊥平面 ABC,ABC=120,四边形 BCC1B1为正方形,且 AB=BC=2,则异面直线BC1与 AC 所成角的余弦值为_____.16.已知集合,,则_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在平面直角坐标系 xOy 中,直线 l 的参数方程为(t 为参数),以坐标原点 O 为极点,x轴的正半轴为极轴建立极坐标系,圆 C 的极坐标方程为. (1)求直线 l 的普通方程和圆 C 的直角坐标方程;(2)直线 l 与圆 C 交于 A,B 两点,点 P(2,1),求|PA| |⋅ PB|的值.18.(12 分)已知为等差数列,为等比数列,的前 n 项和为,满足,,,.(1)求数列和的通项公式;(2)令,数列的前 n 项和,求.19.(12 分)如图,在四棱锥中,底面是直角梯形且∥,侧面为等边三角形,且平面平面.(1)求平面与平面所成的锐二面角的大小;(2)若,且直线与平面所成角为,求的值.20.(12 分)设数列是等差数列,其前项和为,且,.(1)求数列的通项公式;(2)证明:.21.(12 分)如图,已知四边形的直角梯形,...