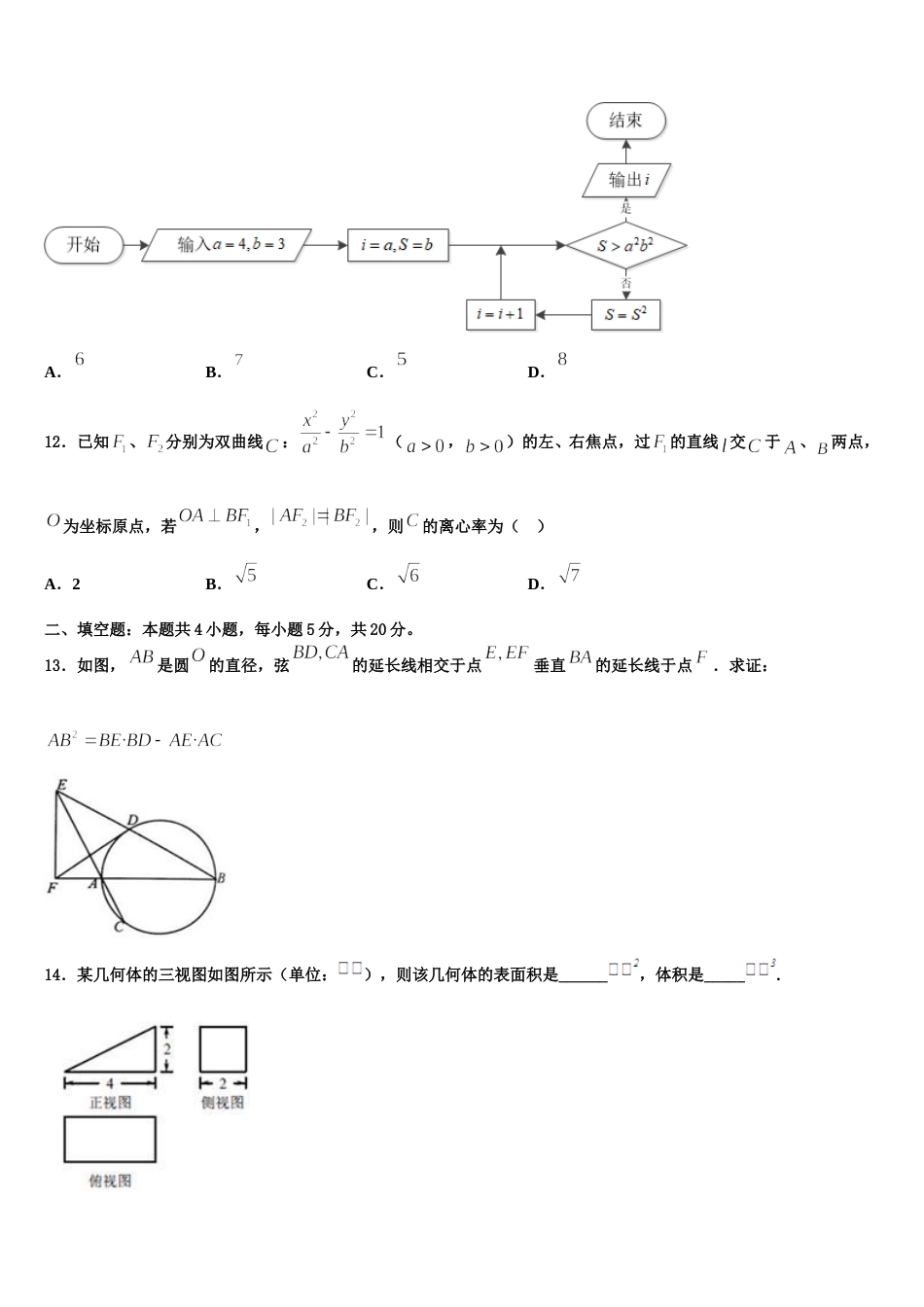
宁夏自治区育才中学 2023-2024 学年高考压轴卷数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.数列{an}是等差数列,a1=1,公差 d∈[1,2],且 a4+λa10+a16=15,则实数 λ 的最大值为( )A.B.C.D.2.已知,,,若,则( )A.B.C.D.3.已知不同直线 、与不同平面、,且,,则下列说法中正确的是( )A.若,则B.若,则C.若,则D.若,则4.已知斜率为的直线与双曲线交于两点,若为线段中点且(为坐标原点),则双曲线的离心率为( )A.B.3C.D.5.设,,则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件6.抛物线的焦点为 F,点为该抛物线上的动点,若点,则的最小值为( )A.B.C.D.7.用电脑每次可以从区间内自动生成一个实数,且每次生成每个实数都是等可能性的.若用该电脑连续生成 3 个实数,则这 3 个实数都小于 的概率为( )A.B.C.D.8.如图,在中,点为线段上靠近点的三等分点,点为线段上靠近点的三等分点,则( )A.B.C.D.9.如果,那么下列不等式成立的是( )A.B.C.D.10.在中,点为中点,过点的直线与,所在直线分别交于点,,若,,则的最小值为( )A.B.2C.3D.11.如图所示的程序框图,若输入,,则输出的结果是( )A.B.C.D.12.已知、分别为双曲线:(,)的左、右焦点,过的直线 交于、两点,为坐标原点,若,,则的离心率为( )A.2B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,是圆的直径,弦的延长线相交于点垂直的延长线于点.求证:14.某几何体的三视图如图所示(单位:),则该几何体的表面积是______,体积是_____.15.设随机变量服从正态分布,若,则的值是______.16.在平面直角坐标系中,已知圆及点,设点是圆上的动点,在中,若的角平分线与相交于点,则的取值范围是_______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图所示,直角梯形中,,,,四边形为矩形,.(1)求证:平面平面;(2)在线段上是否存在点,使得直线与平面所成角的正弦值为,若存在,求出线段的长,若不存在,请说明理由.18.(12 分)在中,.(Ⅰ)求角的大小;(Ⅱ)若,,求的值.19.(12 分)在中,内角所对的边分别为,已知,且.(I)求角的大小;(Ⅱ)若,求面积的取值范围.20.(12 分)如图,三棱柱中,侧面是菱形,其对角线的交点为,且.(1)求证:平面;(2)设,若直线与平面所成的角为,求二面角的正弦值.21.(12 分)已知抛物线 C:x24py(p 为大于 2 的质数)的焦点为 F,过点 F 且斜率为 k(k0)的直线交 C 于 A,B 两点,线段 AB 的垂直平分线交 y 轴于点 E,抛物线 C 在点 A,B 处的切线相交于点 G.记四边形 AEBG 的面积为 S.(1)求点 G 的轨迹方程;(2)当点 G 的横坐标为整数时,S 是否为整数?若是,请求出所有满足条件的 S 的值;若不是,请说明理由.22.(10 分)已知数列的各项均为正数,且满足.(1)求,及的通项公式;(2)求数列的前项和.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】利用等差数列通项公式推导出 λ,由 d∈[1,2],能求出实数 λ 取最大值.【详解】 数列{an}是等差数列,a1=1,公差 d∈[1,2],且 a4+λa10+a16=15,∴1+3d+λ(1+9d)+1+15d=15,解得 λ,d ∈[1,2],λ2是减函数,d∴ =1 时,实数 λ 取最大值为 λ.故选 D.【点睛】本题考查实数值的最大值的求法,考查等差数列的性质等基础知识,考...