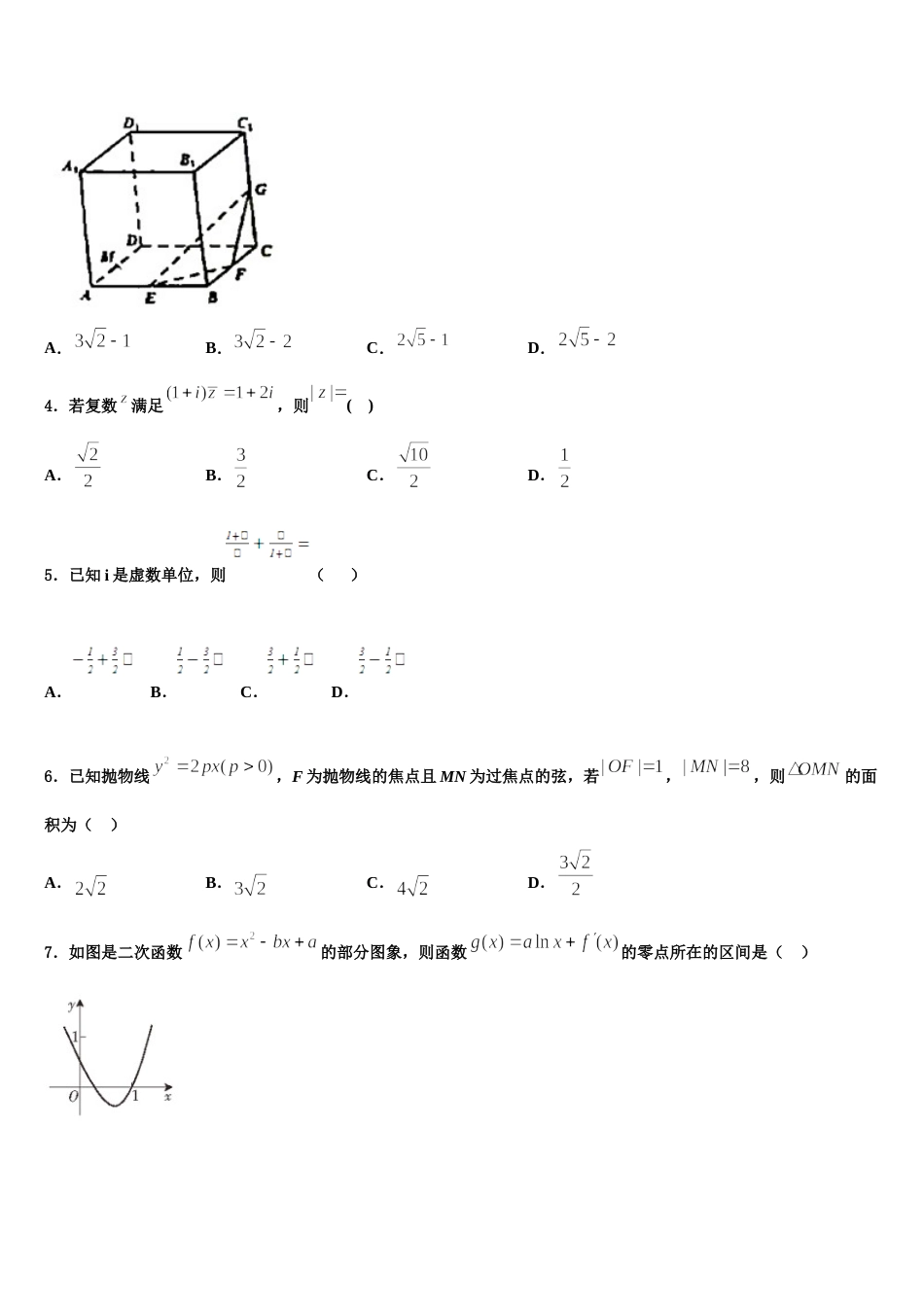
安康市重点中学 2023-2024 学年高考考前提分数学仿真卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用 2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在复平面内,复数 z=i 对应的点为 Z,将向量绕原点 O 按逆时针方向旋转,所得向量对应的复数是( )A.B.C.D.2.网络是一种先进的高频传输技术,我国的技术发展迅速,已位居世界前列.华为公司 2019 年 8 月初推出了一款手机,现调查得到该款手机上市时间和市场占有率(单位:%)的几组相关对应数据.如图所示的折线图中,横轴 1 代表 2019 年 8 月,2 代表 2019 年 9 月……,5 代表 2019 年 12 月,根据数据得出关于的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款手机市场占有率能超过 0.5%(精确到月)( )A.2020 年 6 月B.2020 年 7 月C.2020 年 8 月D.2020 年 9 月3.如图,在棱长为 4 的正方体中,E,F,G 分别为棱 AB,BC,的中点,M 为棱 AD 的中点,设 P,Q 为底面 ABCD 内的两个动点,满足平面 EFG,,则的最小值为( )A.B.C.D.4.若复数满足,则( )A.B.C.D.5.已知 i 是虚数单位,则( )A. B. C. D.6.已知抛物线,F 为抛物线的焦点且 MN 为过焦点的弦,若,,则的面积为( )A.B.C.D.7.如图是二次函数的部分图象,则函数的零点所在的区间是( )A.B.C.D.8.已知直线与直线则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.已知,则下列说法中正确的是( )A.是假命题B.是真命题C.是真命题D.是假命题10.抛掷一枚质地均匀的硬币,每次正反面出现的概率相同,连续抛掷 5 次,至少连续出现 3 次正面朝上的概率是( )A.B.C.D.11.从装有除颜色外完全相同的 3 个白球和个黑球的布袋中随机摸取一球,有放回的摸取 5 次,设摸得白球数为,已知,则 A.B.C.D.12.若函数的图象过点,则它的一条对称轴方程可能是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.某外商计划在个候选城市中投资 个不同的项目,且在同一个城市投资的项目不超过个,则该外商不同的投资方案有____种.14.以,为圆心的两圆均过,与轴正半轴分别交于,,且满足,则点的轨迹方程为_________.15.已知,复数且( 为虚数单位),则__________,_________.16.满足约束条件的目标函数的最小值是 . 三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知椭圆的离心率为,且过点.(1)求椭圆 C 的标准方程;(2)点 P 是椭圆上异于短轴端点 A,B 的任意一点,过点 P 作轴于 Q,线段 PQ 的中点为 M.直线 AM 与直线交于点 N,D 为线段 BN 的中点,设 O 为坐标原点,试判断以 OD 为直径的圆与点 M 的位置关系.18.(12 分)已知函数,,使得对任意两个不等的正实数,都有恒成立.(1)求的解析式;(2)若方程有两个实根,且,求证:.19.(12 分)已知曲线:和:(为参数).以原点为极点,轴的正半轴为极轴,建立极坐标系,且两种坐标系中取相同的长度单位.(1)求曲线的直角坐标方程和的方程化为极坐标方程;(2)设与,轴交于,两点,且线段的中点为.若射线与,交于,两点,求,两点间的距离.20.(12 分)2019 年 9 月 26 日,携程网发布《2019 国庆假期旅游出行趋势预测报告》,2018 年国庆假日期间,西安共接待游客 1692.56 万人次,今年国庆有望超过 2000 万人次,成为西部省份中接待游客量最多的城市.旅游公司规定:若公司某位导游接待旅客,旅游年总收人不低于 40(单位:万元)...