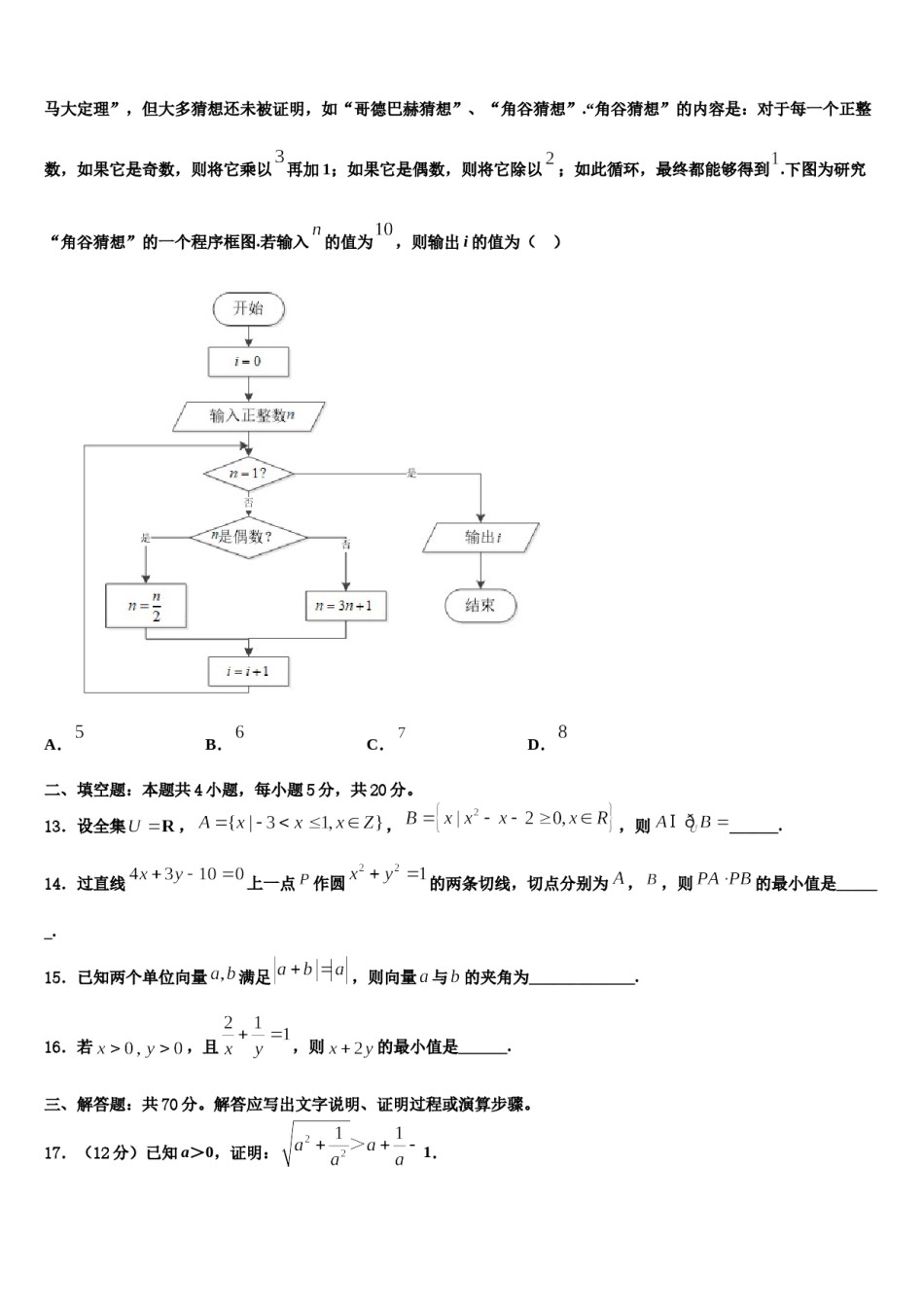
安徽省淮北师范大学附属实验中学2023-2024学年高考适应性考试数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设i是虚数单位,若复数()是纯虚数,则m的值为()A.B.C.1D.32.已知,椭圆的方程,双曲线的方程为,和的离心率之积为,则的渐近线方程为()A.B.C.D.3.某三棱锥的三视图如图所示,网格纸上小正方形的边长为,则该三棱锥外接球的表面积为()A.B.C.D.4.已知函数,若恒成立,则满足条件的的个数为()A.0B.1C.2D.35.设点是椭圆上的一点,是椭圆的两个焦点,若,则()A.B.C.D.6.已知双曲线:的焦距为,焦点到双曲线的渐近线的距离为,则双曲线的渐近线方程为()A.B.C.D.7.设为虚数单位,则复数在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限8.在中,角所对的边分别为,已知,.当变化时,若存在最大值,则正数的取值范围为A.B.C.D.9.函数的单调递增区间是()A.B.C.D.10.函数与在上最多有n个交点,交点分别为(,……,n),则()A.7B.8C.9D.10,11.已知向量与的夹角为,,则()A.B.0C.0或D.12.很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以再加1;如果它是偶数,则将它除以;如此循环,最终都能够得到.下图为研究“角谷猜想”的一个程序框图.若输入的值为,则输出i的值为()A.B.C.D.,则二、填空题:本题共4小题,每小题5分,共20分。13.设全集,,______.14.过直线上一点作圆的两条切线,切点分别为,,则的最小值是______.,则向量与的夹角为_____________.15.已知两个单位向量满足16.若,且,则的最小值是______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知a>0,证明:1.18.(12分)已知圆上有一动点,点的坐标为,四边形为平行四边形,线段的垂直平分线交于点.两点,点的坐标为,直线与轴分别交于两点,(Ⅰ)求点的轨迹的方程;(Ⅱ)过点作直线与曲线交于求证:线段的中点为定点,并求出面积的最大值.19.(12分)已知数列{an}的各项均为正,Sn为数列{an}的前n项和,an2+2an=4Sn+1.(1)求{an}的通项公式;(2)设bn,求数列{bn}的前n项和.20.(12分)如图,在四棱锥中,平面ABCD平面PAD,,,,,E是PD的中点.证明:;设,点M在线段PC上且异面直线BM与CE所成角的余弦值为,求二面角的余弦值.21.(12分)已知函数(I)若讨论的单调性;(Ⅱ)若,且对于函数的图象上两点,存在,使得函数的图象在处的切线.求证:.22.(10分)如图,点是以为直径的圆上异于、的一点,直角梯形所在平面与圆所在平面垂直,且,.(1)证明:平面;(2)求点到平面的距离.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据复数除法运算化简,结合纯虚数定义即可求得m的值.【详解】由复数的除法运算化简可得,因为是纯虚数,所以,∴,故选:A.【点睛】本题考查了复数的概念和除法运算,属于基础题.2、A【解析】根据椭圆与双曲线离心率的表示形式,结合和的离心率之积为,即可得的关系,进而得双曲线的离心率方程.【详解】椭圆的方程,双曲线的方程为,则椭圆离心率,双曲线的离心率,由和的离心率之积为,即,解得,所以渐近线方程为,化简可得,故选:A.【点睛】本题考查了椭圆与双曲线简单几何性质应用,椭圆与双曲线离心率表示形式,双曲线渐近线方程求法,属于基础题.3、C【解析】作出三棱锥...