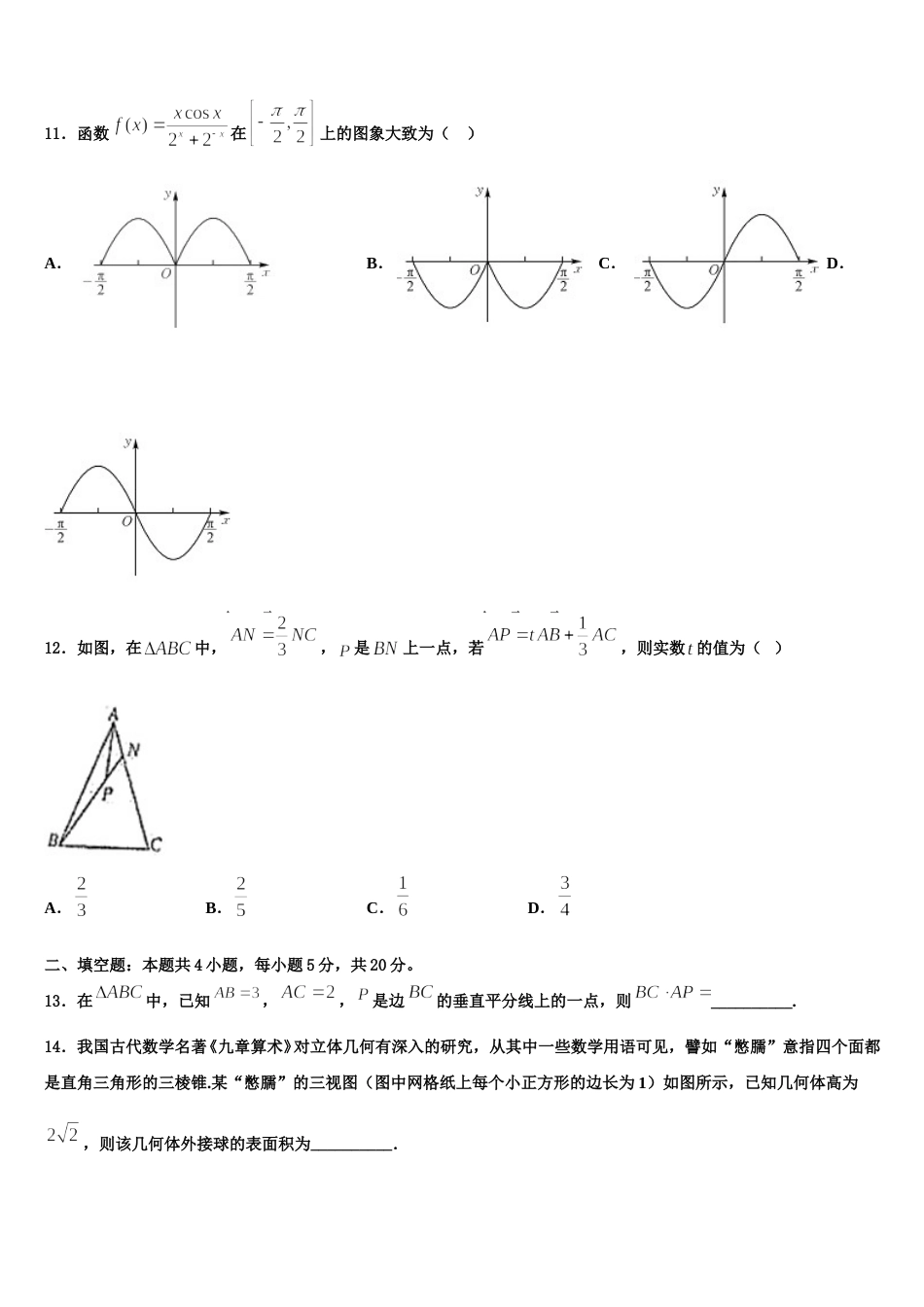
安徽省舒城龙河中学 2024 年高考数学必刷试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.甲在微信群中发了一个 6 元“拼手气”红包,被乙 丙 丁三人抢完、、,若三人均领到整数元,且每人至少领到 1 元,则乙获得“最佳手气”(即乙领到的钱数多于其他任何人)的概率是( )A.B.C.D.2.已知,则,不可能满足的关系是()A.B.C.D.3.是正四面体的面内一动点,为棱中点,记与平面成角为定值,若点的轨迹为一段抛物线,则( )A.B.C.D.4.函数在上的最大值和最小值分别为( )A.,-2B.,-9C.-2,-9D.2,-25.已知平面向量满足,且,则所夹的锐角为( )A.B.C.D.06.已知随机变量 X 的分布列如下表:X01Pabc其中 a,b,.若 X 的方差对所有都成立,则( )A.B.C.D.7.已知等差数列的前项和为,若,则等差数列公差( )A.2B.C.3D.48.已知 P 是双曲线渐近线上一点,,是双曲线的左、右焦点,,记,PO,的斜率为,k,,若,-2k,成等差数列,则此双曲线的离心率为( )A.B.C.D.9.设 i 是虚数单位,若复数是纯虚数,则 a 的值为( )A.B.3C.1D.10.2019 年末,武汉出现新型冠状病毒肺炎()疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从 2 月 7 日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户 6 口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为()且相互独立,该家庭至少检测了 5 个人才能确定为“感染高危户”的概率为,当时,最大,则( )A.B.C.D.11.函数在上的图象大致为( )A. B. C. D. 12.如图,在中,,是上一点,若,则实数 的值为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在中,已知,,是边的垂直平分线上的一点,则__________.14.我国古代数学名著《九章算术》对立体几何有深入的研究,从其中一些数学用语可见,譬如“憋臑”意指四个面都是直角三角形的三棱锥.某“憋臑”的三视图(图中网格纸上每个小正方形的边长为 1)如图所示,已知几何体高为,则该几何体外接球的表面积为__________.15.已知函数在上单调递增,则实数 a 值范围为_________.16.已知数列满足:,,若对任意的正整数均有,则实数的最大值是_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数,(1)若,求的单调区间和极值;(2)设,且有两个极值点,,若,求的最小值.18.(12 分)已知函数是自然对数的底数.(1)若,讨论的单调性;(2)若有两个极值点,求的取值范围,并证明:.19.(12 分)已知函数(1)当时,证明,在恒成立;(2)若在处取得极大值,求的取值范围.20.(12 分)心形线是由一个圆上的一个定点,当该圆在绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名,在极坐标系中,方程()表示的曲线就是一条心形线,如图,以极轴所在的直线为轴,极点为坐标原点的直角坐标系中.已知曲线的参数方程为( 为参数).(1)求曲线的极坐标方程;(2)若曲线与相交于、、三点,求线段的长.21.(12 分)如图:在中,,,.(1)求角;(2)...