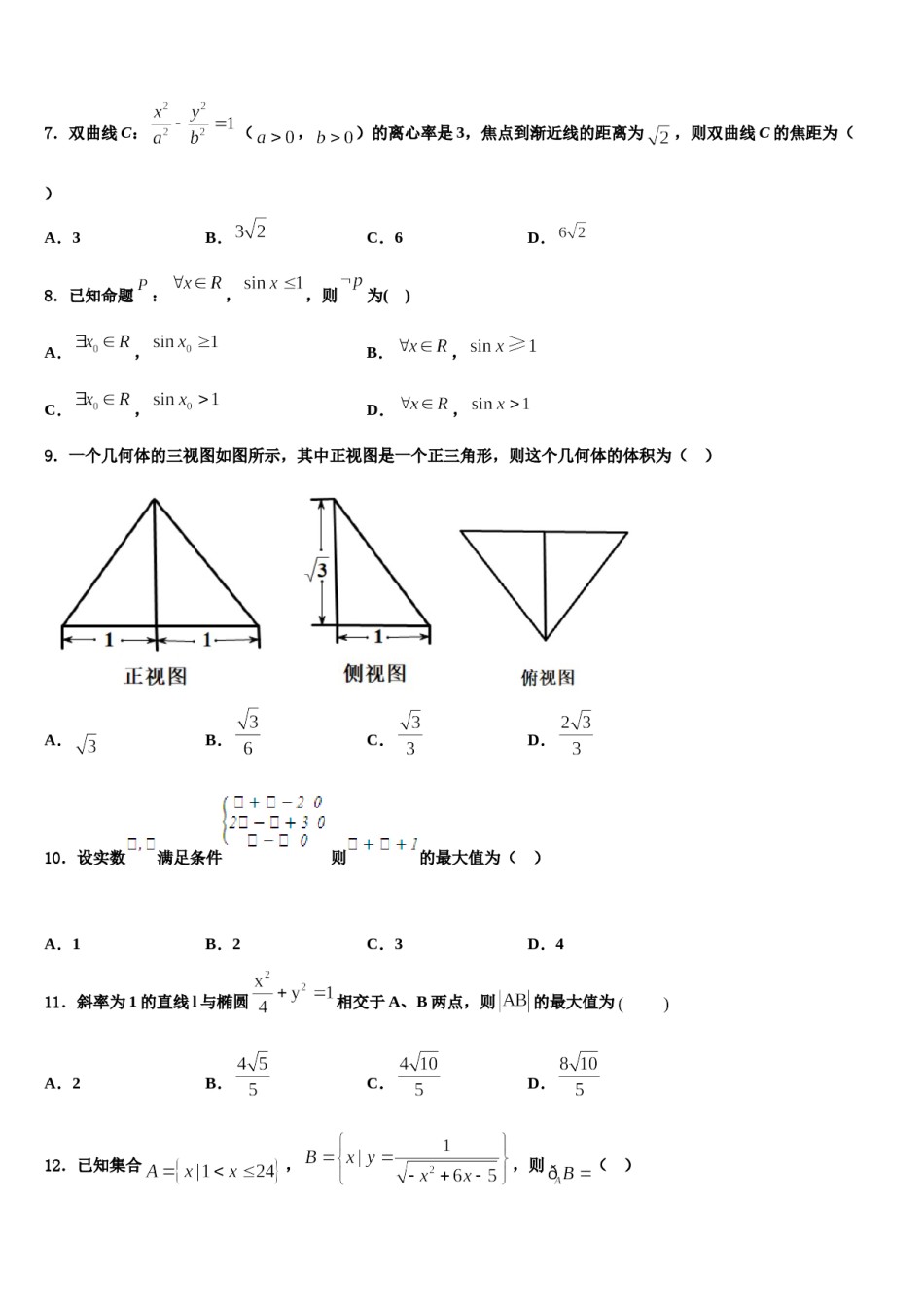
安徽省蚌埠市禹会区北京师范大学蚌埠附属学校2024年高三第二次诊断性检测数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数,则在上不单调的一个充分不必要条件可以是()A.B.C.或D.2.已知向量,,若,则与夹角的余弦值为()A.B.C.D.3.已知的面积是,,,则()A.5B.或1C.5或1D.4.中国古代数学著作《算法统宗》中有这样一个问题;“三百七十八里关,初行健步不为难,次后脚痛递减半,六朝才得到其关,要见每朝行里数,请公仔细算相还.”其意思为:“有一个人走了378里路,第一天健步走行,从第二天起脚痛每天走的路程是前一天的一半,走了6天后到达目的地,求该人每天走的路程.”由这个描述请算出这人第四天走的路程为()A.6里B.12里C.24里D.48里5.已知直线与圆有公共点,则的最大值为()A.4B.C.D.6.在边长为1的等边三角形中,点E是中点,点F是中点,则()A.B.C.D.7.双曲线C:(,)的离心率是3,焦点到渐近线的距离为,则双曲线C的焦距为()A.3B.C.6D.8.已知命题:,,则为()A.,B.,C.,D.,9.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为()A.B.C.D.10.设实数满足条件则的最大值为()A.1B.2C.3D.411.斜率为1的直线l与椭圆相交于A、B两点,则的最大值为A.2B.C.D.12.已知集合,,则()A.B.C.或D.二、填空题:本题共4小题,每小题5分,共20分。13.正方体的棱长为2,是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),为正方体表面上的动点,当弦的长度最大时,的取值范围是______.14.设是等比数列的前项的和,成等差数列,则的值为_____.15.在三棱锥中,,,两两垂直且,点为的外接球上任意一点,则的最大值为______.16.已知,则______,______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知圆,定点,为平面内一动点,以线段为直径的圆内切于圆,设动点的轨迹为曲线(1)求曲线的方程(2)过点的直线与交于两点,已知点,直线分别与直线交于两点,线段的中点是否在定直线上,若存在,求出该直线方程;若不是,说明理由.18.(12分)如图1,四边形是边长为2的菱形,,为的中点,以为折痕将折起到的位置,使得平面平面,如图2.(1)证明:平面平面;(2)求点到平面的距离.19.(12分)已知函数,且曲线在处的切线方程为.(1)求的极值点与极值.(2)当,时,证明:.20.(12分)已知数列满足:,,且对任意的都有,(Ⅰ)证明:对任意,都有;;(Ⅱ)证明:对任意,都有(Ⅲ)证明:.21.(12分)已知直线的参数方程为(,为参数),曲线的极坐标方程为.(1)将曲线的极坐标方程化为直角坐标方程,并说明曲线的形状;(2)若直线经过点,求直线被曲线截得的线段的长.22.(10分)的内角A,B,C的对边分别为a,b,c,已知,.求C;若,求,的面积参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】先求函数在上不单调的充要条件,即在上有解,即可得出结论.【详解】,若在上不单调,令,则函数对称轴方程为在区间上有零点(可以用二分法求得).当时,显然不成立;当时,只需或,解得或.故选:D.【点睛】本题考查含参数的函数的单调性及充分不必要条件,要注意二次函数零点的求法,属于中档题.2、B【解析】直接利用向量的坐标运算得到向量的坐标,利用求得参数m,再用计算即可.【详解】,而,即,解得,则依题意,.故选:B.【点睛】本题考查向量的坐标运算、向量数量积的应用,考查运算求解能力以及化归与转化思想.3、B【解析】 ,,∴①若为钝角,则,由余弦定理得,解得;②若为锐角,则,同理得.故选B.,求出4、C【解析】设第一天走里,则是...