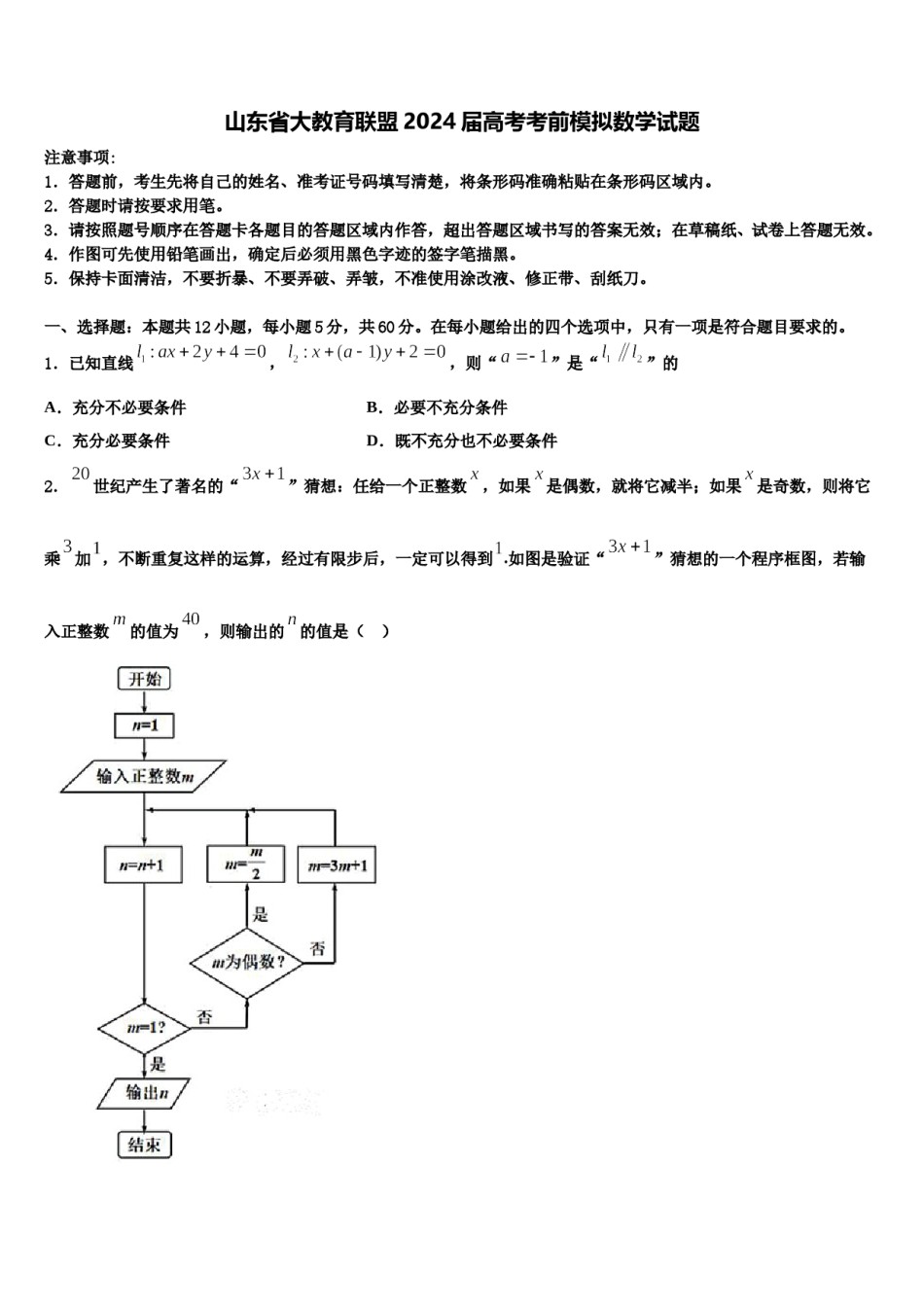
山东省大教育联盟2024届高考考前模拟数学试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知直线,,则“”是“”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2.世纪产生了著名的“”猜想:任给一个正整数,如果是偶数,就将它减半;如果是奇数,则将它乘加,不断重复这样的运算,经过有限步后,一定可以得到.如图是验证“”猜想的一个程序框图,若输入正整数的值为,则输出的的值是()A.B.C.D.3.《九章算术》勾股章有一“引葭赴岸”问题“今有饼池径丈,葭生其中,出水两尺,引葭赴岸,适与岸齐,问水深,葭各几何?”,其意思是:有一个直径为一丈的圆柱形水池,池中心生有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多高?其中一丈等于十尺,如图若从该葭上随机取一点,则该点取自水下的概率为()A.B.C.D.4.已知函数,存在实数,使得,则的最大值为()A.B.C.D.5.在中所对的边分别是,若,则()D.A.37B.13C.6.若表示不超过的最大整数(如,,),已知,,,则()A.2B.5C.7D.87.如图,在沿着AM翻折成中,点M是边的中点,将,且点不在平面内,点是线段上一点.若二面角与二面角的平面角相等,则直线经过的()A.重心B.垂心C.内心D.外心有实根”,若为真命题的充分不必要条件为8.已知命题:“关于的方程,则实数的取值范围是()A.B.C.D.9.设为锐角,若,则的值为()A.B.C.D.10.若,则的值为()A.B.C.D.11.设,则"是""的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件12.从抛物线上一点(点在轴上方)引抛物线准线的垂线,垂足为,且,设抛物线的焦点为,则直线的斜率为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.设定义域为的函数满足,则不等式的解集为__________.14.已知平面向量,的夹角为,且,则=____15.在三棱锥中,三条侧棱两两垂直,,则三棱锥外接球的表面积的最小值为________.16.若展开式的二项式系数之和为64,则展开式各项系数和为__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数在上的最大值为3.(1)求的值及函数的单调递增区间;(2)若锐角中角所对的边分别为,且,求的取值范围.18.(12分)的内角,,的对边分别为,,已知,.(1)求;(2)若的面积,求.19.(12分)已知函数,.(Ⅰ)求的最小正周期;(Ⅱ)求在上的最小值和最大值.20.(12分)已知矩阵,二阶矩阵满足.以为极点,轴正半轴为极轴建立极坐标系,(1)求矩阵;(2)求矩阵的特征值.21.(12分)在直角坐标系中,曲线的参数方程为设点在曲线上,点在曲线上,且为正三角形.(1)求点,的极坐标;的中点,求的最大值.(2)若点为曲线上的动点,为线段22.(10分)已知函数,曲线在点处的切线方程为求a,b的值;证明:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】先得出两直线平行的充要条件,根据小范围可推导出大范围,可得到答案.【详解】直线,,的充要条件是,当a=2时,化简后发现两直线是重合的,故舍去,最终a=-1.因此得到“”是“”的充分必要条件.故答案为C.【点睛】判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假...