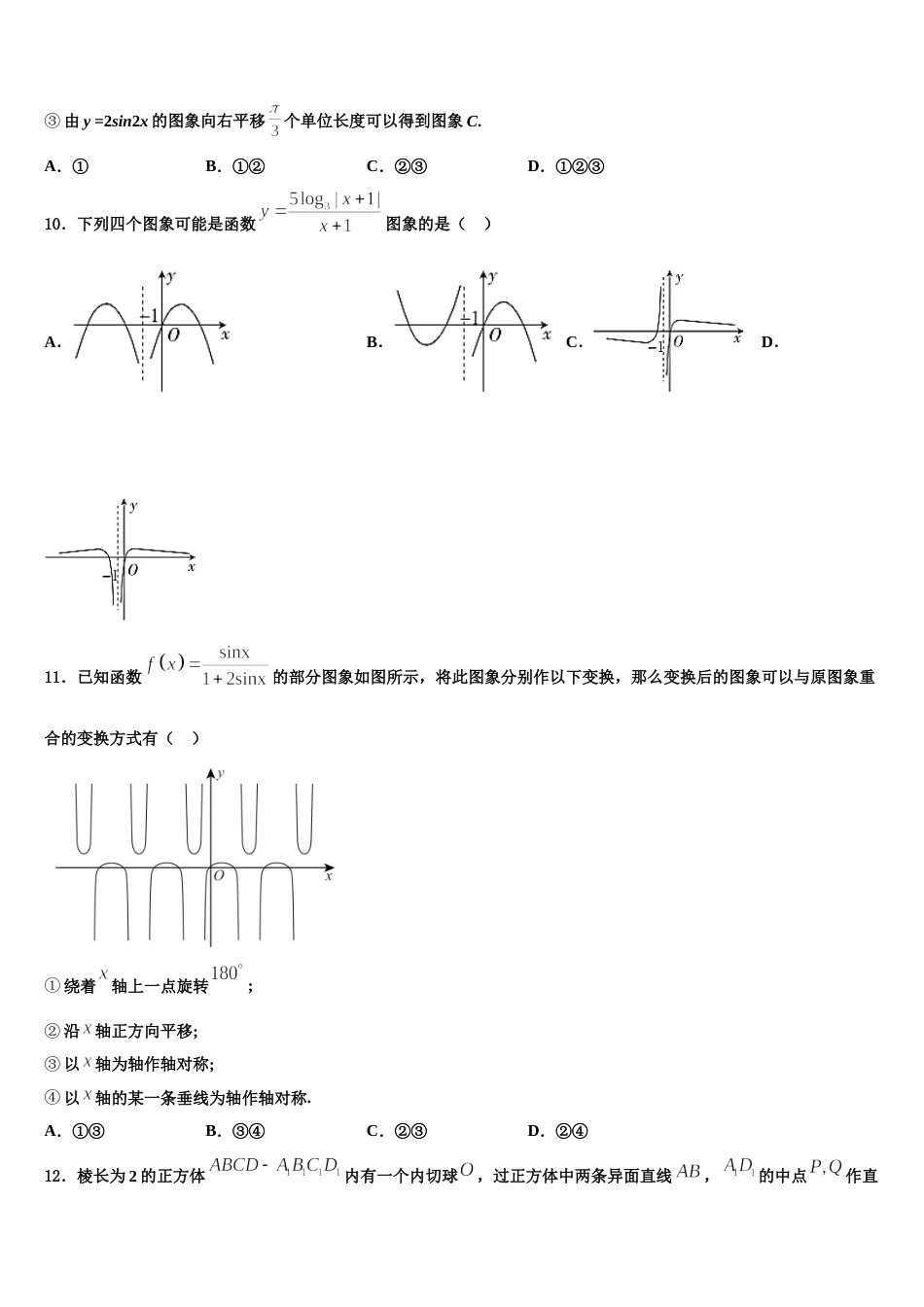
山东省胶州市第一中学 2023-2024 学年高考数学二模试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设函数,则,的大致图象大致是的( )A.B.C.D.2.定义,已知函数,,则函数的最小值为( )A.B.C.D.3.对于任意,函数满足,且当时,函数.若,则大小关系是( )A.B.C.D.4. 是虚数单位,复数在复平面上对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限5.集合中含有的元素个数为( )A.4B.6C.8D.126.在等差数列中,若为前项和,,则的值是( )A.156B.124C.136D.1807.等腰直角三角形的斜边 AB 为正四面体侧棱,直角边 AE 绕斜边 AB 旋转,则在旋转的过程中,有下列说法:(1)四面体 EBCD 的体积有最大值和最小值;(2)存在某个位置,使得;(3)设二面角的平面角为,则;(4)AE 的中点 M 与 AB 的中点 N 连线交平面 BCD 于点 P,则点 P 的轨迹为椭圆.其中,正确说法的个数是( )A.1B.2C.3D.48.已知定义在上的奇函数满足,且当时,,则( )A.1B.-1C.2D.-29.函数的图象为 C,以下结论中正确的是( )① 图象 C 关于直线对称;② 图象 C 关于点对称;③ 由 y =2sin2x 的图象向右平移个单位长度可以得到图象 C.A.①B.①②C.②③D.①②③10.下列四个图象可能是函数图象的是( )A.B.C.D.11.已知函数的部分图象如图所示,将此图象分别作以下变换,那么变换后的图象可以与原图象重合的变换方式有( )① 绕着轴上一点旋转; ② 沿轴正方向平移;③ 以轴为轴作轴对称;④ 以轴的某一条垂线为轴作轴对称.A.①③B.③④C.②③D.②④12.棱长为 2 的正方体内有一个内切球,过正方体中两条异面直线,的中点作直线,则该直线被球面截在球内的线段的长为( )A.B.C.D.1二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知数列满足对任意,若,则数列的通项公式________.14.的展开式中项的系数为_______.15.在棱长为的正方体中,是正方形的中心,为的中点,过的平面与直线垂直,则平面截正方体所得的截面面积为______.16.已知函数,令,,若,表示不超过实数的最大整数,记数列的前项和为,则_________三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)中国古代数学经典《数书九章》中,将底面为矩形且有一条侧棱与底面垂直的四棱锥称为“阳马”,将四个面都为直角三角形的四面体称之为“鳖臑”.在如图所示的阳马中,底面 ABCD 是矩形.平面,,,以的中点 O 为球心,AC 为直径的球面交 PD 于 M(异于点 D),交 PC于 N(异于点 C).(1)证明:平面,并判断四面体 MCDA 是否是鳖臑,若是,写出它每个面的直角(只需写出结论);若不是,请说明理由;(2)求直线与平面所成角的正弦值.18.(12 分)如图,四棱锥 P﹣ABCD 的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,,(Ⅰ)证明;AC⊥BP;(Ⅱ)求直线 AD 与平面 APC 所成角的正弦值.19.(12 分)已知函数.(Ⅰ)若,求曲线在处的切线方程;(Ⅱ)当时,要使恒成立,求实数的取值范围.20.(12 分)如图,在四棱锥中,底面是直角梯形且∥,侧面为等边三角形,且平面平面.(1)求平面与平面所成的锐二面角的大小;(2)若,且直线与平面所成角为,求的值.21.(12 分)如图,在四棱柱中,平面,底面 ABCD 满足∥BC,且( )Ⅰ 求证:平面;()Ⅱ 求直线与平面所成角的正弦值.22.(10 分)已知函数,其中为实常数.(1)若存在,使得在区间内单调递减,求的取值范围;(2)当时,设...