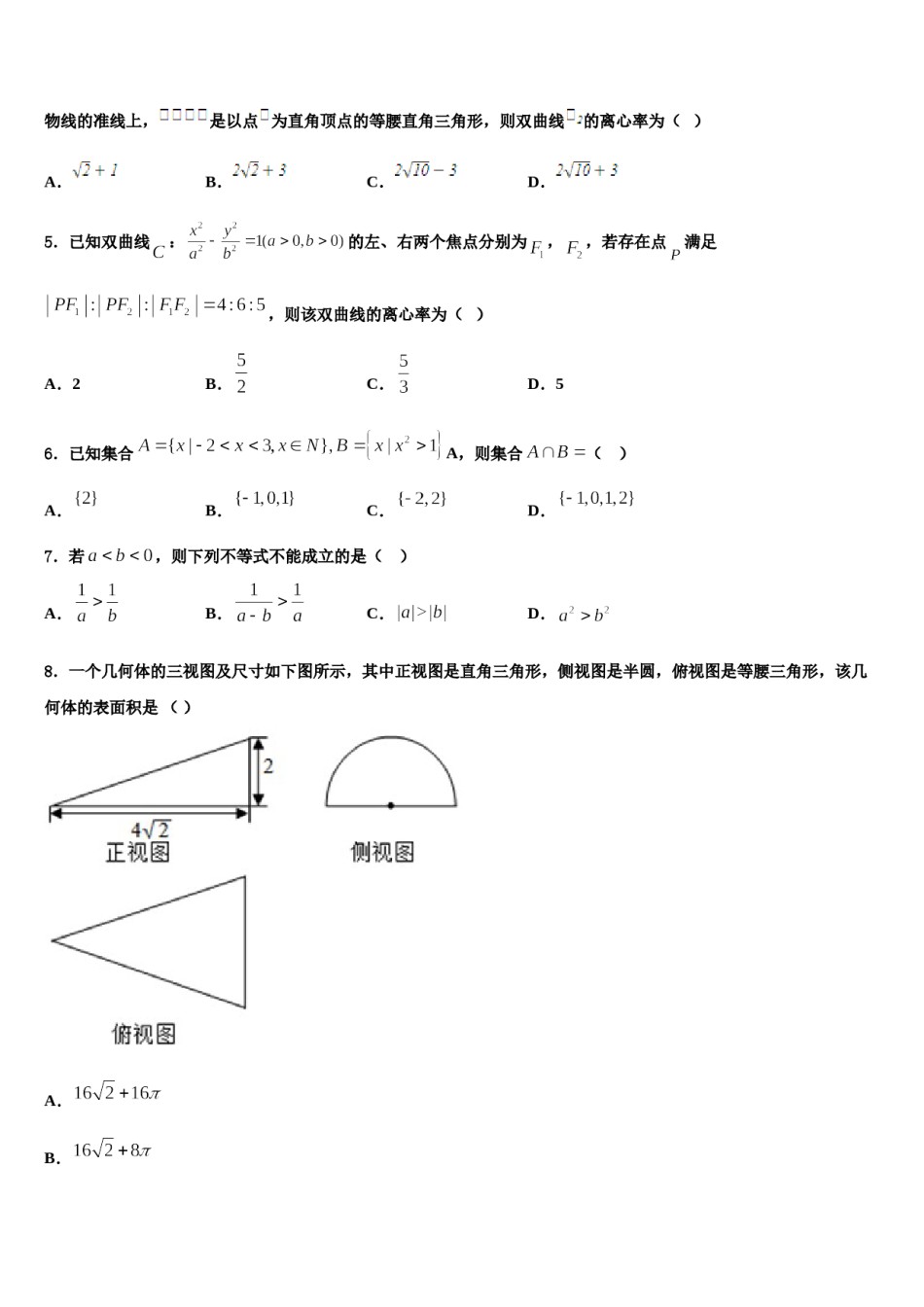
山东省诸城市2024年高三第四次模拟考试数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数(即质数)的和”,如,.在不超过20的素数中,随机选取两个不同的数,其和等于20的概率是()A.B.C.D.以上都不对2.在复平面内,复数z=i对应的点为Z,将向量绕原点O按逆时针方向旋转,所得向量对应的复数是()A.B.C.D.3.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数且能构成等差数列的概率为()A.B.C.D.4.抛物线的焦点是双曲线的右焦点,点是曲线的交点,点在抛物线的准线上,是以点为直角顶点的等腰直角三角形,则双曲线的离心率为()A.B.C.D.5.已知双曲线:的左、右两个焦点分别为,,若存在点满足,则该双曲线的离心率为()A.2B.C.D.56.已知集合A,则集合()A.B.C.D.7.若,则下列不等式不能成立的是()A.B.C.D.8.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是()A.B.C.,则()D.9.若复数z满足A.B.C.D.10.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的体积为()A.B.C.D.11.若为虚数单位,则复数在复平面上对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限12.已知双曲线的左、右焦点分别为,,P是双曲线E上的一点,且.若直线与双曲线E的渐近线交于点M,且M为的中点,则双曲线E的渐近线方程为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.的展开式中二项式系数最大的项的系数为_________(用数字作答).14.的展开式中常数项是___________.15.设,则______.),则16.已知函数,若方程的解为,(_______;_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)眼保健操是一种眼睛的保健体操,主要是通过按摩眼部穴位,调整眼及头部的血液循环,调节肌肉,改善眼的疲劳,达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果,在应届高三的全体800名学生中随机抽取了100名学生进行视力检查,并得到如图的频率分布直方图.(1)若直方图中后三组的频数成等差数列,试估计全年级视力在5.0以上的人数;(2)为了研究学生的视力与眼保健操是否有关系,对年级不做眼保健操和坚持做眼保健操的学生进行了调查,得到下表中数据,根据表中的数据,能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系?(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取8人,进一步调查他们良好的护眼习惯,在这8人中任取2人,记坚持做眼保健操的学生人数为X,求X的分布列和数学期望.附:0.100.050.0250.0100.005k2.7063.8415.0246.6357.87918.(12分)在中,角的对边分别为,且,.(1)求的值;(2)若求的面积.19.(12分)已知椭圆经过点,离心率为.(1)求椭圆的方程;(2)经过点且斜率存在的直线交椭圆于两点,点与点关于坐标原点对称.连接.求证:存在实数,使得成立.20.(12分)已知抛物线的焦点为,点在抛物线上,,直线过点,且与抛物线交于,两点.(1)求抛物线的方程及点的坐标;(2)求的最大值.21.(12分)在①,②,③这三个条件中任选一个,补充在下面问题中,求的面积的值(或最大值).已知的内角,...