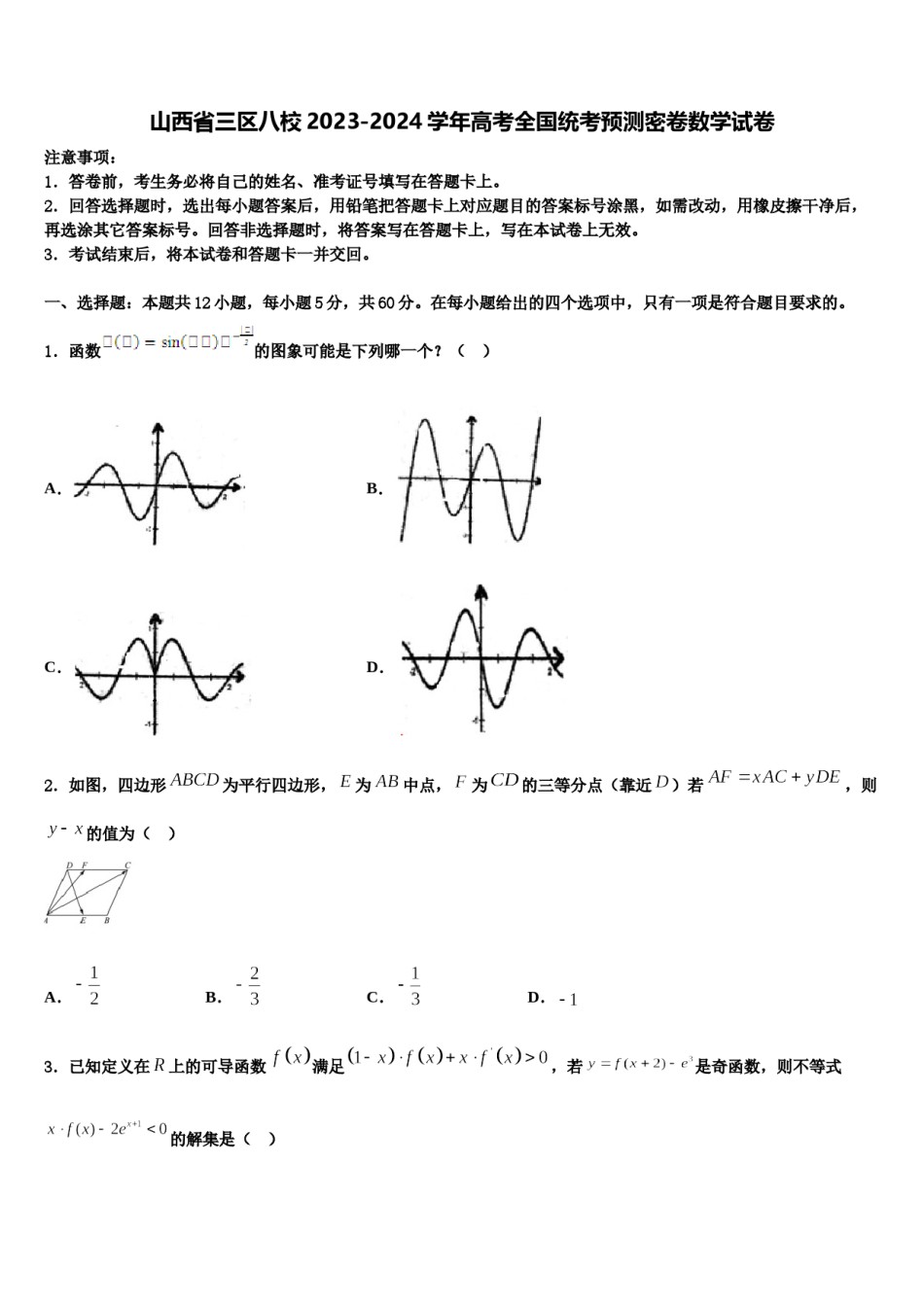
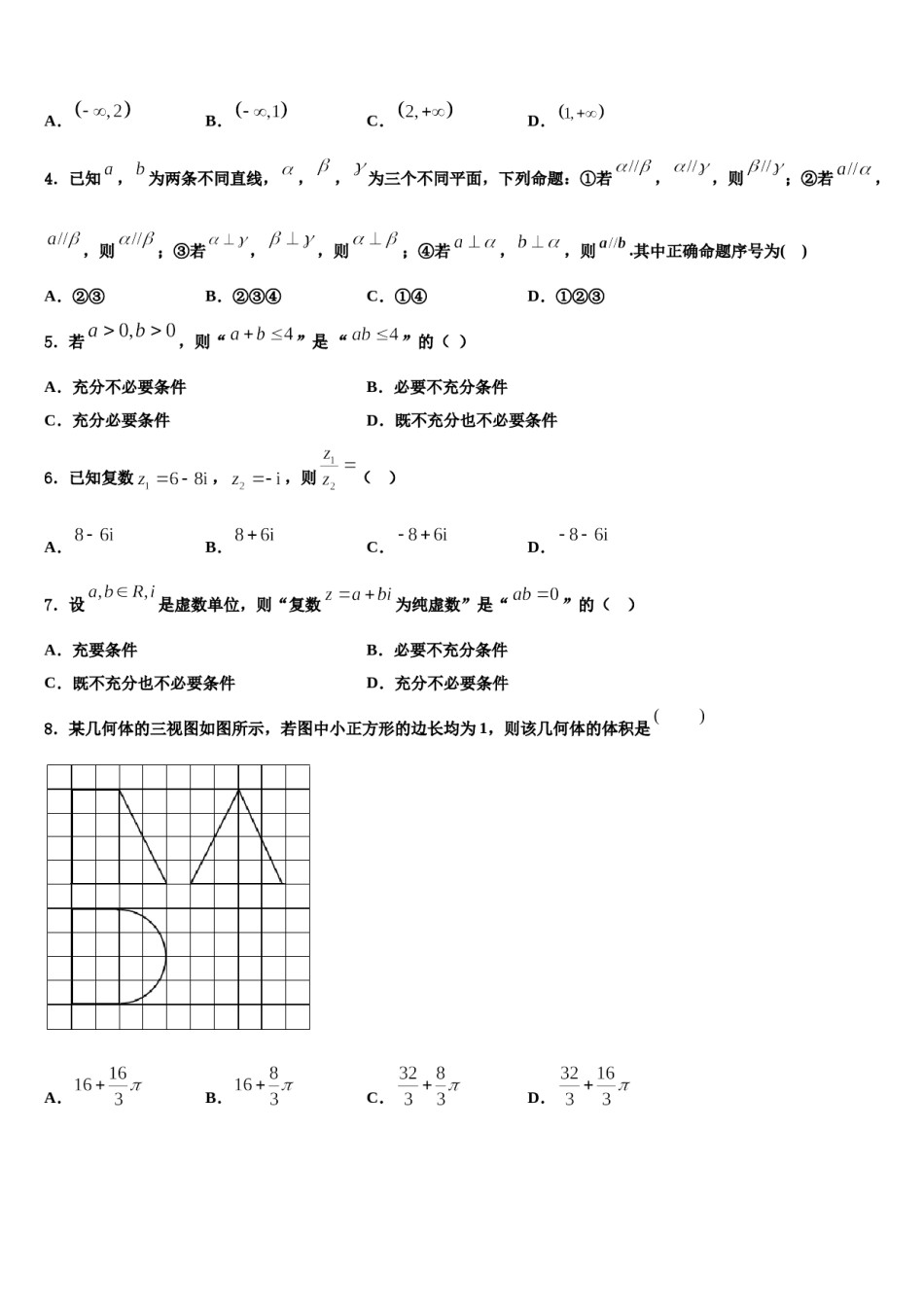
山西省三区八校2023-2024学年高考全国统考预测密卷数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的图象可能是下列哪一个?()A.B.C.D.2.如图,四边形为平行四边形,为中点,为的三等分点(靠近)若,则的值为()A.B.C.D.,若3.已知定义在上的可导函数满足是奇函数,则不等式的解集是()A.B.C.D.4.已知,为两条不同直线,,,为三个不同平面,下列命题:①若,,则;②若,,则;③若,,则;④若,,则.其中正确命题序号为()A.②③B.②③④C.①④D.①②③5.若,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.已知复数,,则()A.B.C.D.7.设是虚数单位,则“复数为纯虚数”是“”的()A.充要条件B.必要不充分条件C.既不充分也不必要条件D.充分不必要条件8.某几何体的三视图如图所示,若图中小正方形的边长均为1,则该几何体的体积是A.B.C.D.9.是的()条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要10.已知随机变量的分布列是则()A.B.C.D.11.已知复数,则对应的点在复平面内位于()A.第一象限B.第二象限C.第三象限D.第四象限12.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式).A.2寸B.3寸C.4寸D.5寸二、填空题:本题共4小题,每小题5分,共20分。13.如果复数满足,那么______(为虚数单位).14.已知F为抛物线C:x2=8y的焦点,P为C上一点,M(﹣4,3),则△PMF周长的最小值是_____.15.近年来,新能源汽车技术不断推陈出新,新产品不断涌现,在汽车市场上影响力不断增大.动力蓄电池技术作为新能源汽车的核心技术,它的不断成熟也是推动新能源汽车发展的主要动力.假定现在市售的某款新能源汽车上,车载动力蓄电池充放电循环次数达到2000次的概率为85%,充放电循环次数达到2500次的概率为35%.若某用户的自用新能源汽车已经经过了2000次充电,那么他的车能够充电2500次的概率为______.16.在中,,,,则__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图,在三棱柱中,、、分别是、、的中点.(1)证明:平面;(2)若底面是正三角形,,在底面的投影为,求到平面的距离..18.(12分)的内角的对边分别为,且(1)求;(2)若,点为边的中点,且,求的面积.19.(12分)已知椭圆:(),与轴负半轴交于,离心率.(1)求椭圆的方程;(2)设直线:与椭圆交于,两点,连接,并延长交直线于,两点,已知,求证:直线恒过定点,并求出定点坐标.20.(12分)对于给定的正整数k,若各项均不为0的数列满足:对任意正整数总成立,则称数列是“数列”.(1)证明:等比数列是“数列”;(2)若数列既是“数列”又是“数列”,证明:数列是等比数列.21.(12分)设数列是等比数列,,已知,(1)求数列的首项和公比;(2)求数列的通项公式.22.(10分)诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:第二周第三周第四周第一周第一周期第二周期第三周期(Ⅰ)计算表中十二周“水站诚信度”的平均数;(Ⅱ)若定义水站诚信度高于的为“高诚信度”,以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度...