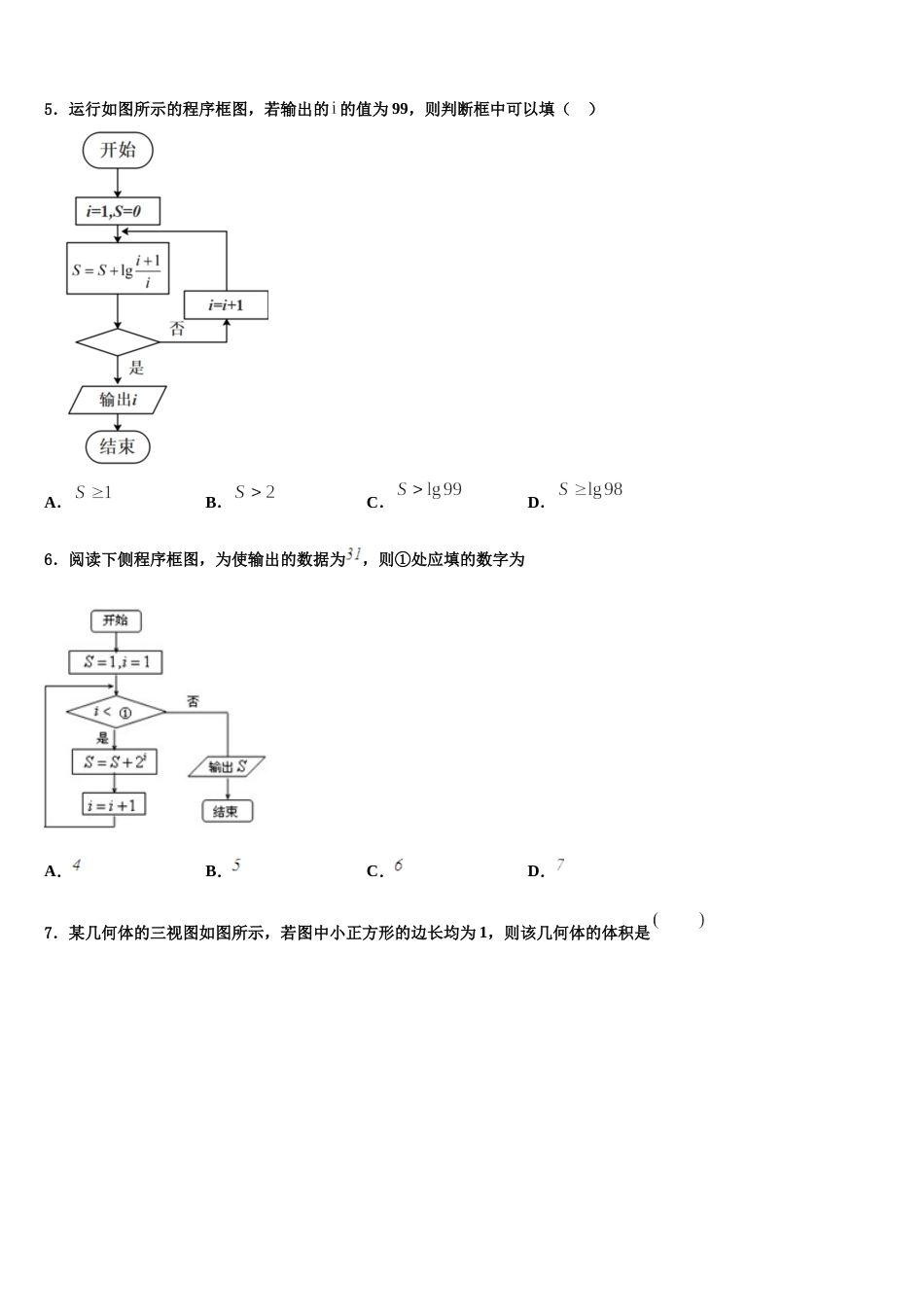
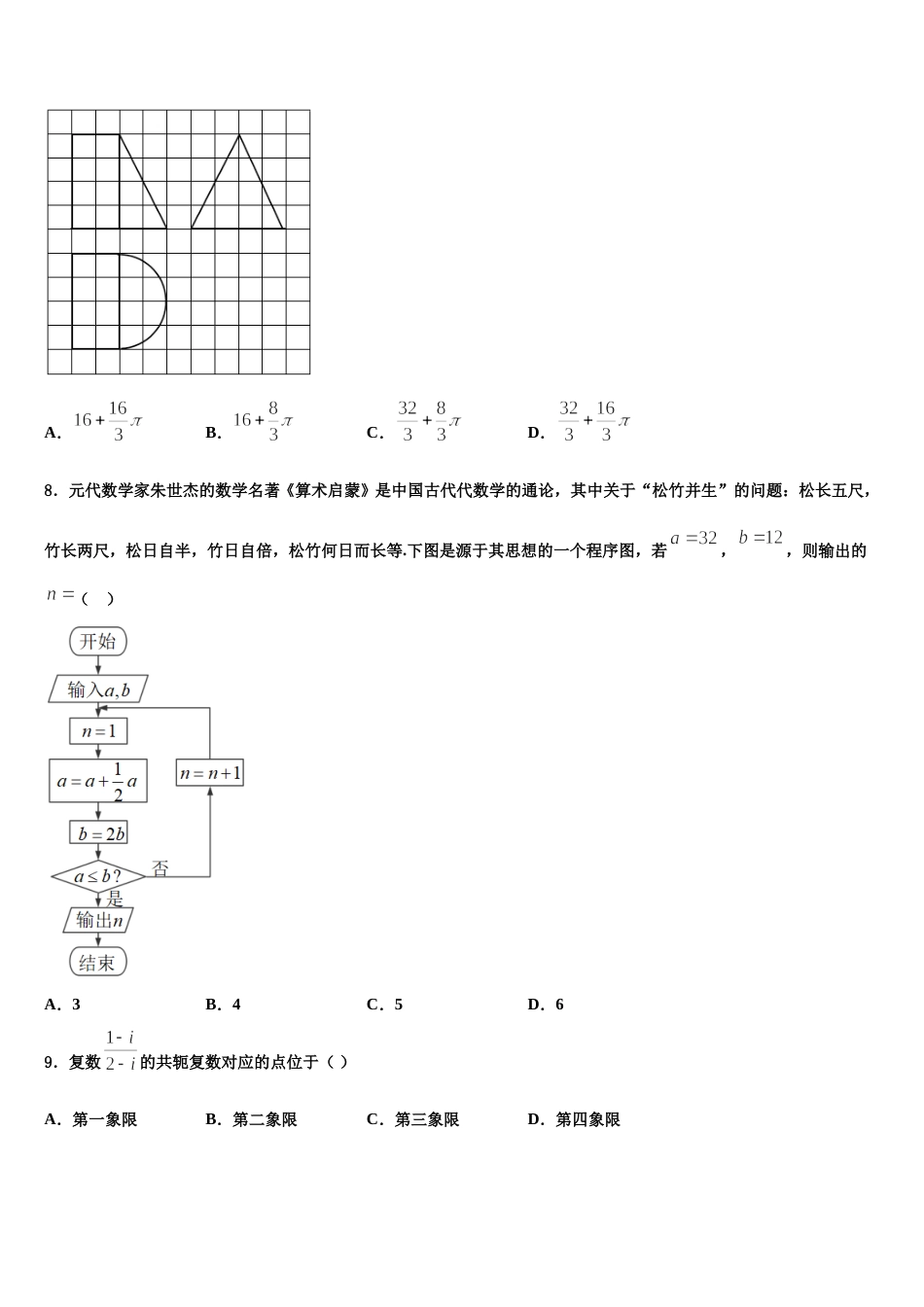
山西省孝义市 2023-2024 学年高三下学期联考数学试题请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知,都是偶函数,且在上单调递增,设函数,若,则( )A.且B.且C.且D.且2.已知是两条不重合的直线,是两个不重合的平面,下列命题正确的是( )A.若,,,,则B.若,,,则C.若,,,则D.若,,,则3.中,,为的中点,,,则( )A.B.C.D.24.已知菱形的边长为 2,,则()A.4B.6C.D.5.运行如图所示的程序框图,若输出的 的值为 99,则判断框中可以填( )A.B.C.D.6.阅读下侧程序框图,为使输出的数据为,则①处应填的数字为A.B.C.D.7.某几何体的三视图如图所示,若图中小正方形的边长均为 1,则该几何体的体积是 A.B.C.D.8.元代数学家朱世杰的数学名著《算术启蒙》是中国古代代数学的通论,其中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序图,若,,则输出的( )A.3B.4C.5D.69.复数的共轭复数对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限10. 为虚数单位,则的虚部为( )A.B.C.D.11.已知函数,,的零点分别为,,,则( )A.B.C.D.12.已知,,是平面内三个单位向量,若,则的最小值( )A.B.C.D.5二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知△ABC 得三边长成公比为的等比数列,则其最大角的余弦值为_____.14.已知函数是定义在上的奇函数,则的值为__________.15.已知向量=(-4,3),=(6,m),且,则 m=__________.16.已知关于的方程在区间上恰有两个解,则实数的取值范围是________三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)有甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司底薪元,送餐员每单制成元;乙公司无底薪,单以内(含单)的部分送餐员每单抽成元,超过单的部分送餐员每单抽成元.现从这两家公司各随机选取一名送餐员,分别记录其天的送餐单数,得到如下频数分布表:送餐单数3839404142甲公司天数101015105乙公司天数101510105(1)从记录甲公司的天送餐单数中随机抽取天,求这天的送餐单数都不小于单的概率;(2)假设同一公司的送餐员一天的送餐单数相同,将频率视为概率,回答下列两个问题:① 求乙公司送餐员日工资的分布列和数学期望;② 小张打算到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,小张应选择哪家公司应聘?说明你的理由.18.(12 分)已知函数,它的导函数为.(1)当时,求的零点;(2)当时,证明:.19.(12 分)已知.(1)解不等式;(2)若均为正数,且,求的最小值.20.(12 分)根据国家统计局数据,1978 年至 2018 年我国 GDP 总量从 0.37 万亿元跃升至 90 万亿元,实际增长了242 倍多,综合国力大幅提升.将年份 1978,1988,1998,2008,2018 分别用 1,2,3,4,5 代替,并表示为 ;表示全国 GDP 总量,表中,.326.4741.90310209.7614.05(1)根据数据及统计图表,判断与(其中为自然对数的底数)哪一个更适宜作为全国 GDP 总量关于 的回归方程类型?(给出判断即可,不必说明理由),并求出关于 的回归方程.(2)使用参考数据,估计 2020 年的全国 GDP 总量.线性回归方程中斜率和截距的最小二乘法估计公式分别为:,.参考数据:45678的近似值551484031097298121.(12 分)唐诗是中国文学的瑰宝.为了研究计算机上唐诗分类工作中检索关键字的选取,某研究人员将唐诗分成 7大类别,并从《全唐诗》48900 多篇唐诗中随机抽取了 500 篇,统计了每个类别及各类别包含“花”、“山”、“帘”字的篇数,得到下表:爱...