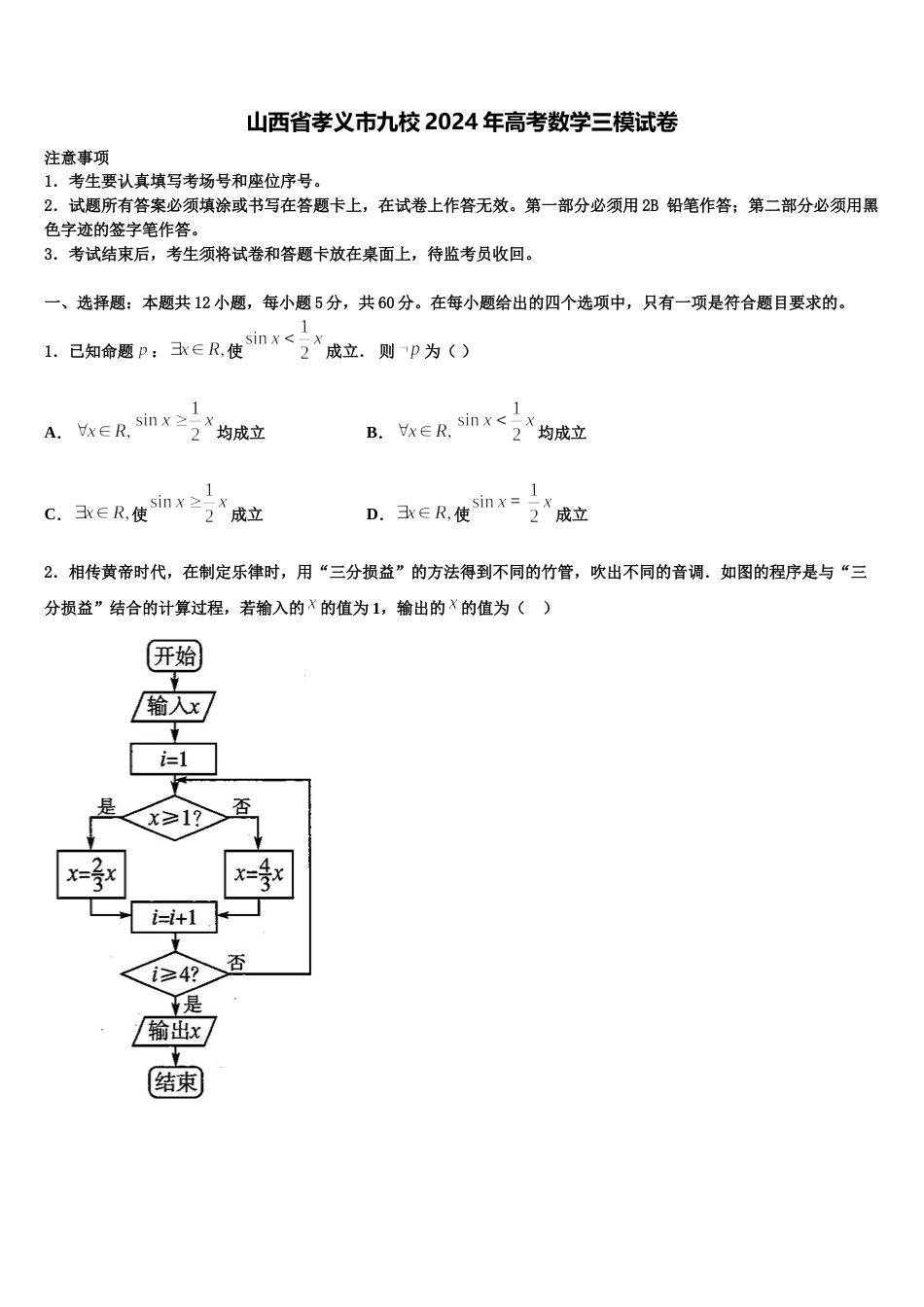
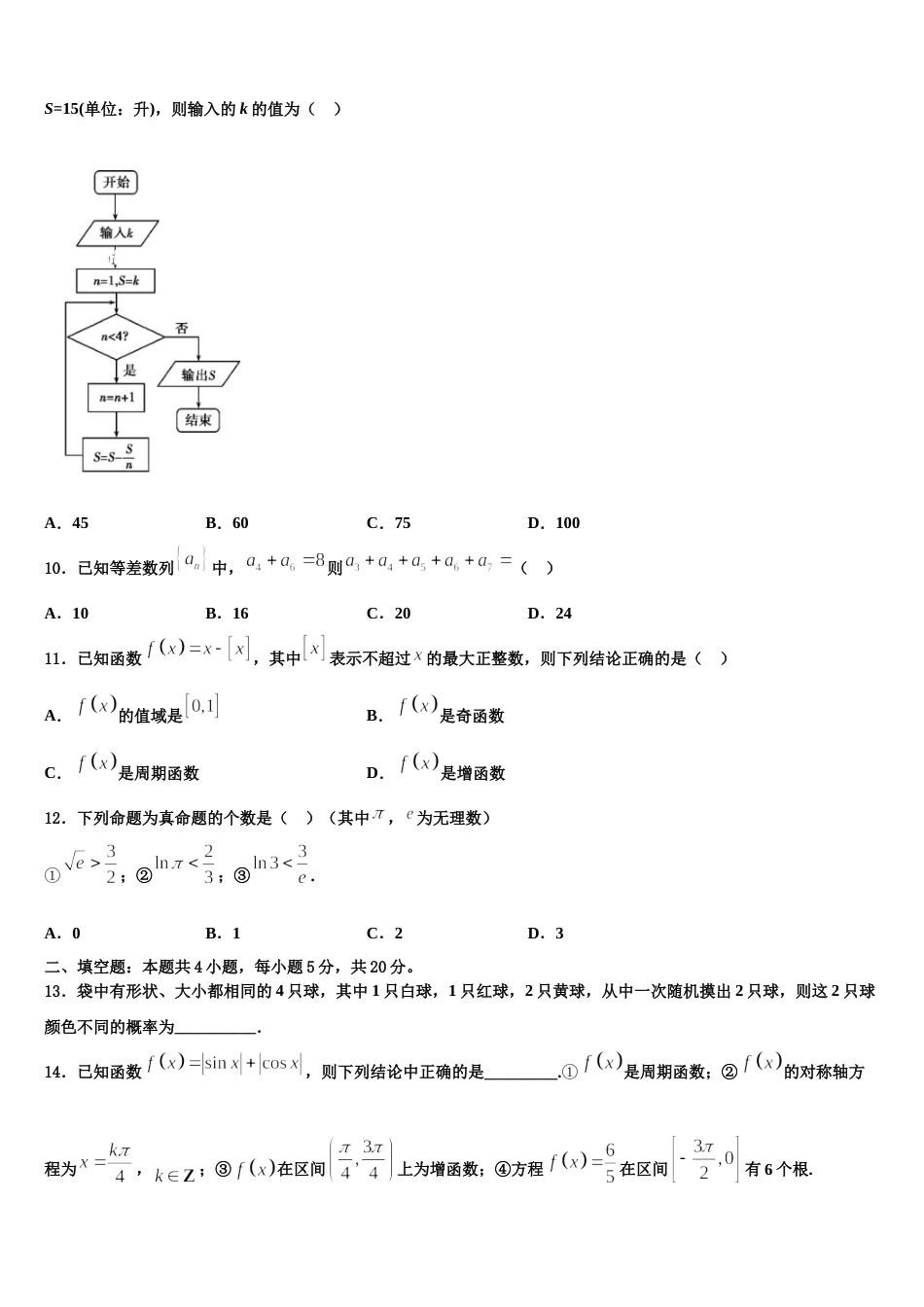
山西省孝义市九校 2024 年高考数学三模试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知命题:使成立. 则为( )A.均成立B.均成立C.使成立D.使成立2.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的的值为 1,输出的的值为( )A.B.C.D.3.在中,点为中点,过点的直线与,所在直线分别交于点,,若,,则的最小值为( )A.B.2C.3D.4.已知函数,,则的极大值点为( )A.B.C.D.5.已知集合,,,则( )A.B.C.D.6.命题:的否定为A.B.C.D.7.若 x,y 满足约束条件且的最大值为,则 a 的取值范围是( )A.B.C.D.8.已知复数满足( 是虚数单位),则=( )A.B.C.D.9.我国古代数学著作《九章算术》中有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升(注:一斗为十升).问,米几何?”下图是解决该问题的程序框图,执行该程序框图,若输出的S=15(单位:升),则输入的 k 的值为( ) A.45B.60C.75D.10010.已知等差数列中,则( )A.10B.16C.20D.2411.已知函数,其中表示不超过的最大正整数,则下列结论正确的是( )A.的值域是B.是奇函数C.是周期函数D.是增函数12.下列命题为真命题的个数是( )(其中, 为无理数)①;②;③.A.0B.1C.2D.3二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.袋中有形状、大小都相同的 4 只球,其中 1 只白球,1 只红球,2 只黄球,从中一次随机摸出 2 只球,则这 2 只球颜色不同的概率为__________.14.已知函数,则下列结论中正确的是_________.①是周期函数;②的对称轴方程为,;③在区间上为增函数;④方程在区间有 6 个根.15.某班星期一共八节课(上午、下午各四节,其中下午最后两节为社团活动),排课要求为:语文、数学、外语、物理、化学各排一节,从生物、历史、地理、政治四科中选排一节.若数学必须安排在上午且与外语不相邻(上午第四节和下午第一节不算相邻),则不同的排法有__________种.16.的展开式中,的系数是__________. (用数字填写答案)三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数(1)若对任意恒成立,求实数的取值范围;(2)求证: 18.(12 分)设函数.(1)时,求的单调区间;(2)当时,设的最小值为,若恒成立,求实数 t 的取值范围.19.(12 分)已知,,(1)求的最小正周期及单调递增区间;(2)已知锐角的内角,,的对边分别为,,,且,,求边上的高的最大值.20.(12 分)在①,②,③这三个条件中任选一个,补充在下面问题中,求的面积的值(或最大值).已知的内角,,所对的边分别为,,,三边,,与面积满足关系式:,且 ,求的面积的值(或最大值).21.(12 分)如图,在斜三棱柱中,平面平面,,,,均为正三角形,E 为 AB 的中点.(Ⅰ)证明:平面;(Ⅱ)求斜三棱柱截去三棱锥后剩余部分的体积.22.(10 分)如图,在三棱锥中,,,,平面平面,、分别为、中点.(1)求证:;(2)求二面角的大小.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】试题分析:原命题为特称命题,故其否定为全称命题,即.考点:全称命题.2、B【解析】根据循环语句,输入,执行循环语句即可计算出结果.【详解】输入,由题意执行循环结构程序框图,可得:第 次循环:,,不满足判断条件;第次循环:,,不满足判断条件;第次循环:,,满足判断条件;输出结果.故选:【点睛】本题考查了循环语句的程...