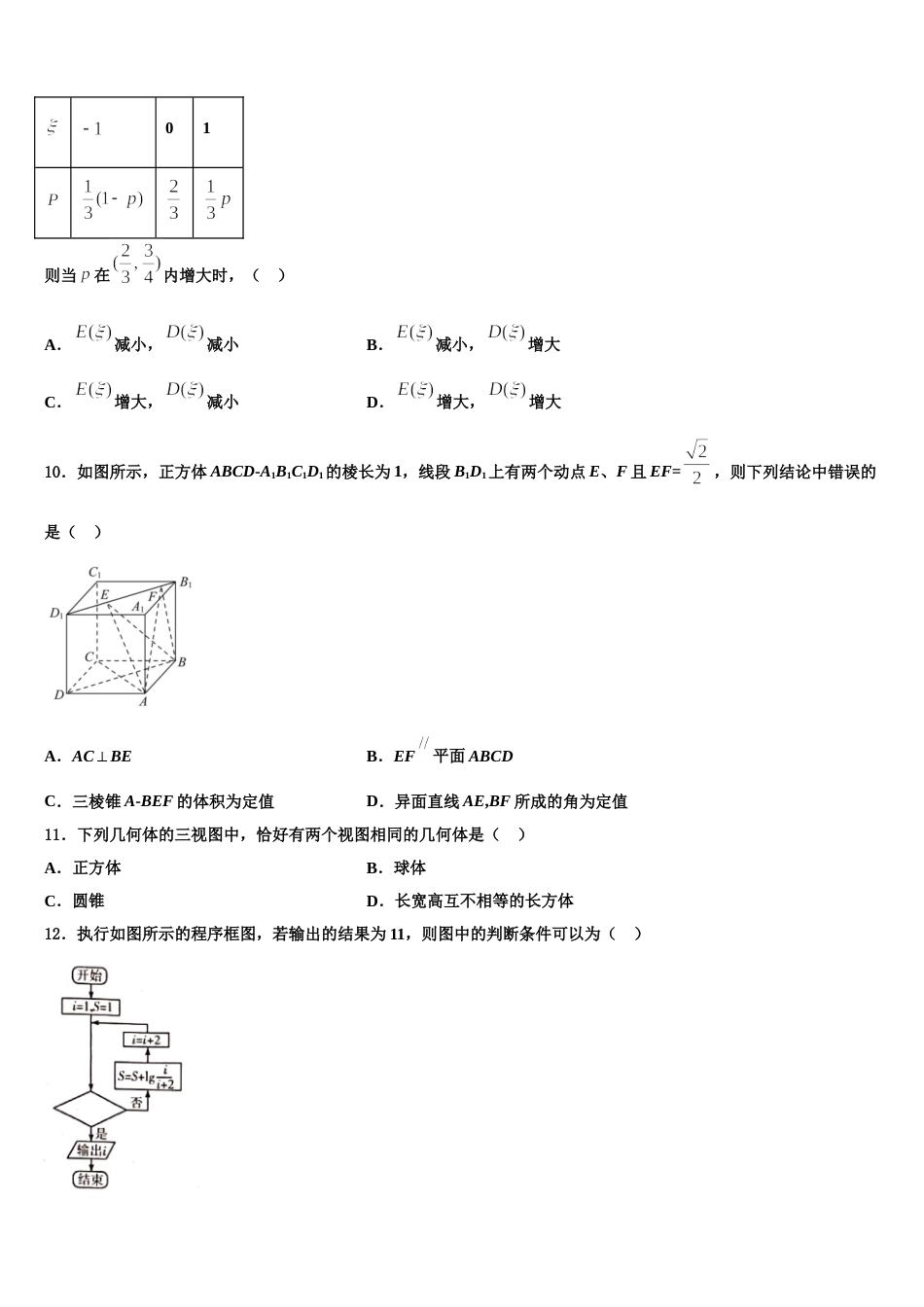
山西省柳林县联盛中学 2023-2024 学年高三(最后冲刺)数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知正四面体的棱长为 ,是该正四面体外接球球心,且,,则( )A.B.C.D.2.已知命题 p:直线 a∥b,且 b⊂平面 α,则 a α∥ ;命题 q:直线 l⊥平面 α,任意直线 mα⊂ ,则 l⊥m.下列命题为真命题的是( )A.p∧qB.p∨(非 q)C.(非 p)∧qD.p∧(非 q)3.已知棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的四个面中,最大面积为( )A.B.C.D.4.如下的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b 分别为 176,320,则输出的 a 为( )A.16B.18C.20D.155.小王因上班繁忙,来不及做午饭,所以叫了外卖.假设小王和外卖小哥都在 12:00~12:10 之间随机到达小王所居住的楼下,则小王在楼下等候外卖小哥的时间不超过 5 分钟的概率是( )A.B.C.D.6.已知函数,当时,的取值范围为,则实数 m的取值范围是( )A.B.C.D.7.已知,椭圆的方程,双曲线的方程为,和的离心率之积为,则的渐近线方程为( )A.B.C.D.8.体育教师指导 4 个学生训练转身动作,预备时,4 个学生全部面朝正南方向站成一排.训练时,每次都让 3 个学生“向后转”,若 4 个学生全部转到面朝正北方向,则至少需要“向后转”的次数是( )A.3B.4C.5D.69.设,随机变量的分布列是01则当在内增大时,( )A.减小,减小B.减小,增大C.增大,减小D.增大,增大10.如图所示,正方体 ABCD-A1B1C1D1的棱长为 1,线段 B1D1上有两个动点 E、F 且 EF=,则下列结论中错误的是( )A.AC⊥BEB.EF平面 ABCDC.三棱锥 A-BEF 的体积为定值D.异面直线 AE,BF 所成的角为定值11.下列几何体的三视图中,恰好有两个视图相同的几何体是( )A.正方体B.球体C.圆锥D.长宽高互不相等的长方体12.执行如图所示的程序框图,若输出的结果为 11,则图中的判断条件可以为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知定义在上的函数的图象关于点对称,,若函数图象与函数图象的交点为,则_____.14.实数,满足约束条件,则的最大值为__________.15.展开式中的系数为_______________.16.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,已知椭圆, 为其右焦点,直线与椭圆交于两点,点在 上,且满足.(点从上到下依次排列)(I)试用表示:(II)证明:原点 到直线 l 的距离为定值.18.(12 分)已知函数,曲线在点处的切线方程为.(1)求,的值;(2)证明函数存在唯一的极大值点,且.19.(12 分)如图,三棱柱的所有棱长均相等,在底面上的投影在棱上,且∥平面(Ⅰ)证明:平面平面;(Ⅱ)求直线与平面所成角的余弦值.20.(12 分) [选修 4-4:极坐标与参数方程] 在直角坐标系中,曲线的参数方程为(是参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线的极坐标方程和曲线的直角坐标方程;(2)若射线与曲线交于,两点,与曲线交于,两点,求取最大值时的值21.(12 分)2019 年入冬时节,长春市民为了迎接 2022 年北京冬奥会,增强身体素质,积极开展冰上体育锻炼.现从速滑项目中随机选出 100 名参与者,并由专业的评估机构对他们的锻炼成果进行评...