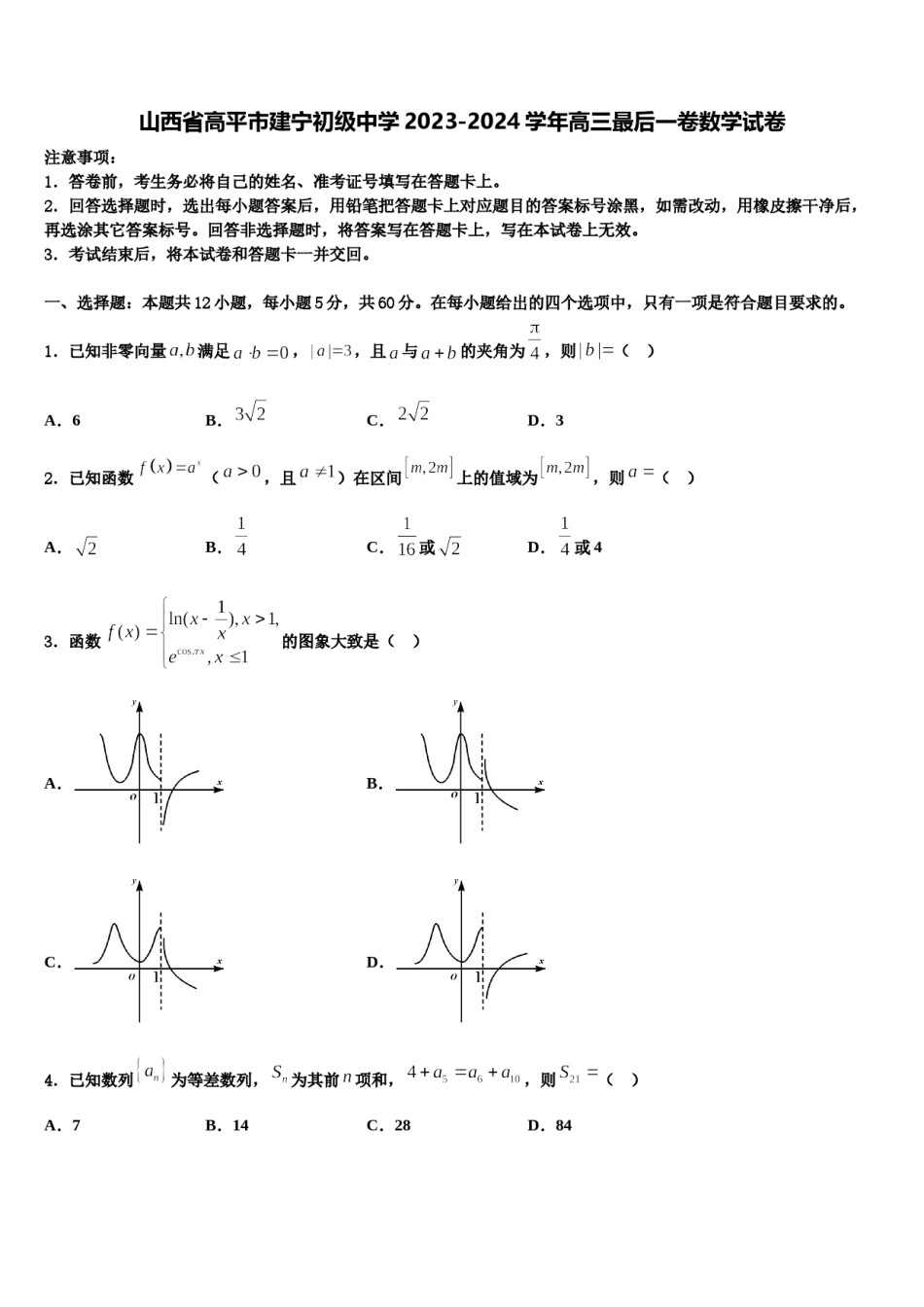
山西省高平市建宁初级中学2023-2024学年高三最后一卷数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知非零向量满足,,且与的夹角为,则()A.6B.C.D.32.已知函数)在区间(,且上的值域为,则()A.B.C.或D.或43.函数的图象大致是()A.B.C.D.4.已知数列为等差数列,为其前项和,,则()A.7B.14C.28D.845.二项式的展开式中只有第六项的二项式系数最大,则展开式中的常数项是()A.180B.90C.45D.3606.已知集合,,,则集合()A.B.C.D.7.木匠师傅对一个圆锥形木件进行加工后得到一个三视图如图所示的新木件,则该木件的体积()A.B.C.D.在上递增,命题在中,8.设命题函数,下列为真命题的是()A.B.C.D.9.设为锐角,若,则的值为()A.B.C.D.10.两圆和相外切,且,则的最大值为()A.B.9C.D.111.已知底面为边长为的正方形,侧棱长为的直四棱柱中,是上底面上的动点.给出以下四个结论中,正确的个数是()①与点距离为的点形成一条曲线,则该曲线的长度是;②若面,则与面所成角的正切值取值范围是;③若,则在该四棱柱六个面上的正投影长度之和的最大值为.A.B.C.D.12.某网店2019年全年的月收支数据如图所示,则针对2019年这一年的收支情况,下列说法中错误的是()A.月收入的极差为60B.7月份的利润最大C.这12个月利润的中位数与众数均为30D.这一年的总利润超过400万元二、填空题:本题共4小题,每小题5分,共20分。13.已知数列满足,且,则______.14.我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程中,p为“隅”,q为“实”.即若的大斜、中斜、小斜分别为a,b,c,则.已知点D是边AB上一点,,,,,则的面积为________.15.已知在等差数列中,,,前n项和为,则________.16.若正实数,,满足,则的最大值是__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数(),不等式的解集为.(1)求的值;(2)若,,,且,求的最大值.18.(12分)已知函数.当时,求不等式的解集;,,求a的取值范围.19.(12分)已知函数.(1)当时,求曲线在点的切线方程;(2)讨论函数的单调性.20.(12分)设都是正数,且,.求证:.21.(12分)已知函数f(x)=x-1+x-2.若不等式a+b+a-b≥af(x)(a≠0,a、b∈R)恒成立,求实数x的取值范围.22.(10分)在中,角,,所对的边分别是,,,且.(1)求的值;(2)若,求的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】利用向量的加法的平行四边形法则,判断四边形的形状,推出结果即可.【详解】解:非零向量,满足,可知两个向量垂直,,且与的夹角为,说明以向量,为邻边,为对角线的平行四边形是正方形,所以则.故选:.【点睛】本题考查向量的几何意义,向量加法的平行四边形法则的应用,考查分析问题解决问题的能力,属于基础题.2、C【解析】对a进行分类讨论,结合指数函数的单调性及值域求解.【详解】分析知,.讨论:当时,,所以,,所以;当时,,所以,,所以.综上,或,故选C.【点睛】本题主要考查指数函数的值域问题,指数函数的值域一般是利用单调性求解,侧重考查数学运算和数学抽象的核心素养.3、A【解析】根据复合函数的单调性,同增异减以及采用...