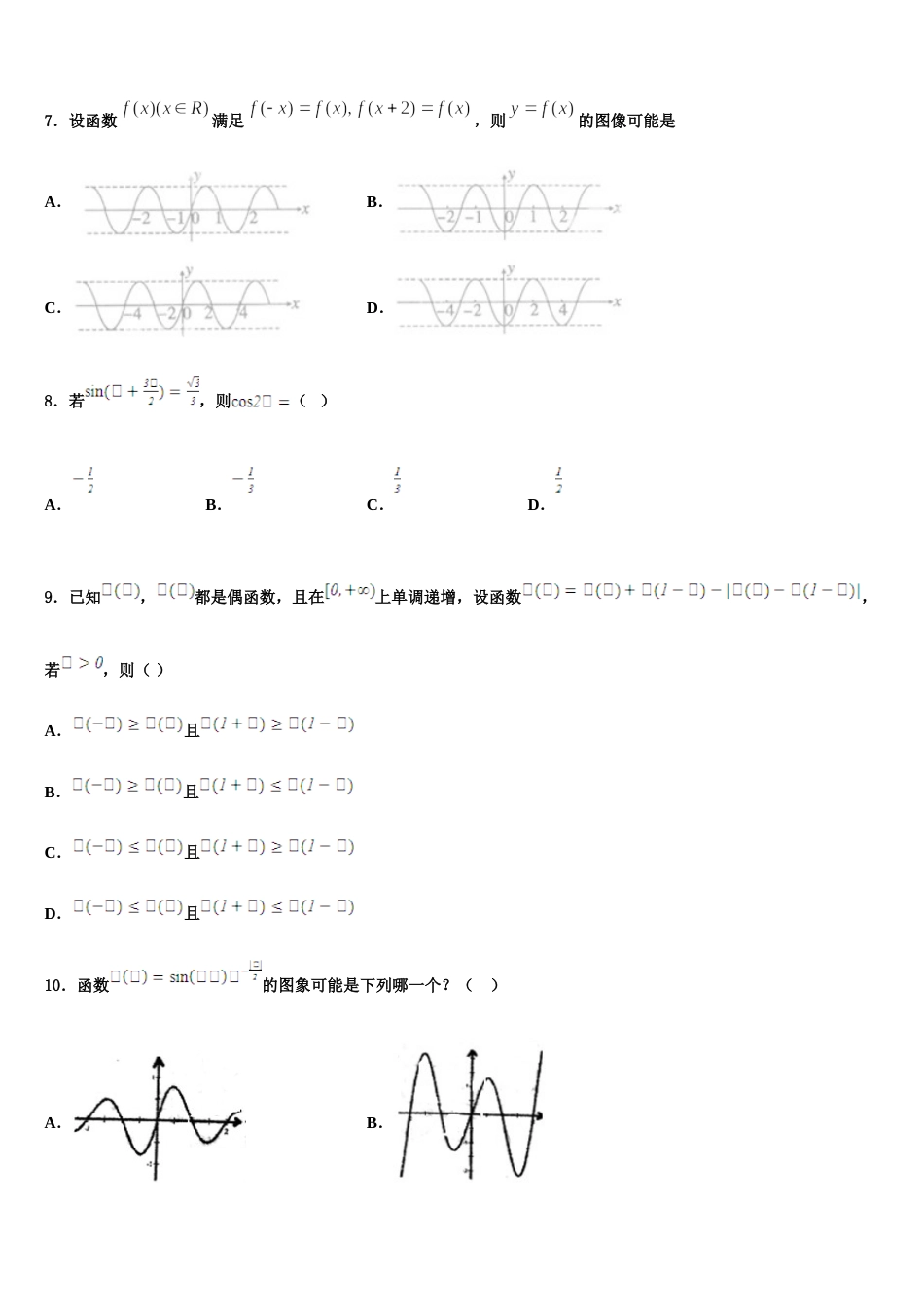
广东省揭阳第一中学 2024 年高考数学三模试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知抛物线,F 为抛物线的焦点且 MN 为过焦点的弦,若,,则的面积为( )A.B.C.D.2.已知复数满足,则的最大值为( )A.B.C.D.63.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,它的终边过点,则的值为( )A.B.C.D.4.设,则“ “是“”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必条件5.已知函数,若关于的方程恰好有 3 个不相等的实数根,则实数的取值范围为( )A.B.C.D.6.已知复数 z 满足,则 z 的虚部为( )A.B.iC.–1D.17.设函数满足,则的图像可能是A.B.C.D.8.若,则( )A.B.C.D.9.已知,都是偶函数,且在上单调递增,设函数,若,则( )A.且B.且C.且D.且10.函数的图象可能是下列哪一个?( )A.B.C.D.11.已知函数(表示不超过 x 的最大整数),若有且仅有 3 个零点,则实数 a的取值范围是( )A.B.C.D.12.在中,,,,为的外心,若,,,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若存在直线 l 与函数及的图象都相切,则实数的最小值为___________.14.从甲、乙等 8 名志愿者中选 5 人参加周一到周五的社区服务,每天安排一人,每人只参加一天.若要求甲、乙两人至少选一人参加,且当甲、乙两人都参加时,他们参加社区服务的日期不相邻,那么不同的安排种数为______________.(用数字作答)15.已知实数满足( 为虚数单位),则的值为_______.16.已知是定义在上的奇函数,当时,,则不等式的解集用区间表示为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知分别是内角的对边,满足(1)求内角的大小(2)已知,设点是外一点,且,求平面四边形面积的最大值.18.(12 分)如图,在多面体中,四边形是菱形,,,,平面,,,是的中点.(Ⅰ)求证:平面平面;(ⅠⅠ)求直线与平面所成的角的正弦值.19.(12 分)设函数,.(1)求函数的极值;(2)对任意,都有,求实数 a 的取值范围.20.(12 分)诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:第一周第二周第三周第四周第一周期第二周期第三周期(Ⅰ)计算表中十二周“水站诚信度”的平均数;(Ⅱ)若定义水站诚信度高于的为“高诚信度”,以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率; (Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.21.(12 分)在三角形中,角,,的对边分别为,,,若.(Ⅰ)求角;(Ⅱ)若,,求.22.(10 分)已知公比为正数的等比数列的前项和为,且,.(1)求数列的通项公式;(2)设,求数列的前项和.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据可知,再利用抛物线的焦半径公式以及三角形面积公式求解即可.【详解】由题意可知抛物线方程为,设点点,则由抛物线定义知,,则.由得,则.又 MN 为过焦点的弦,所以,则,所以....