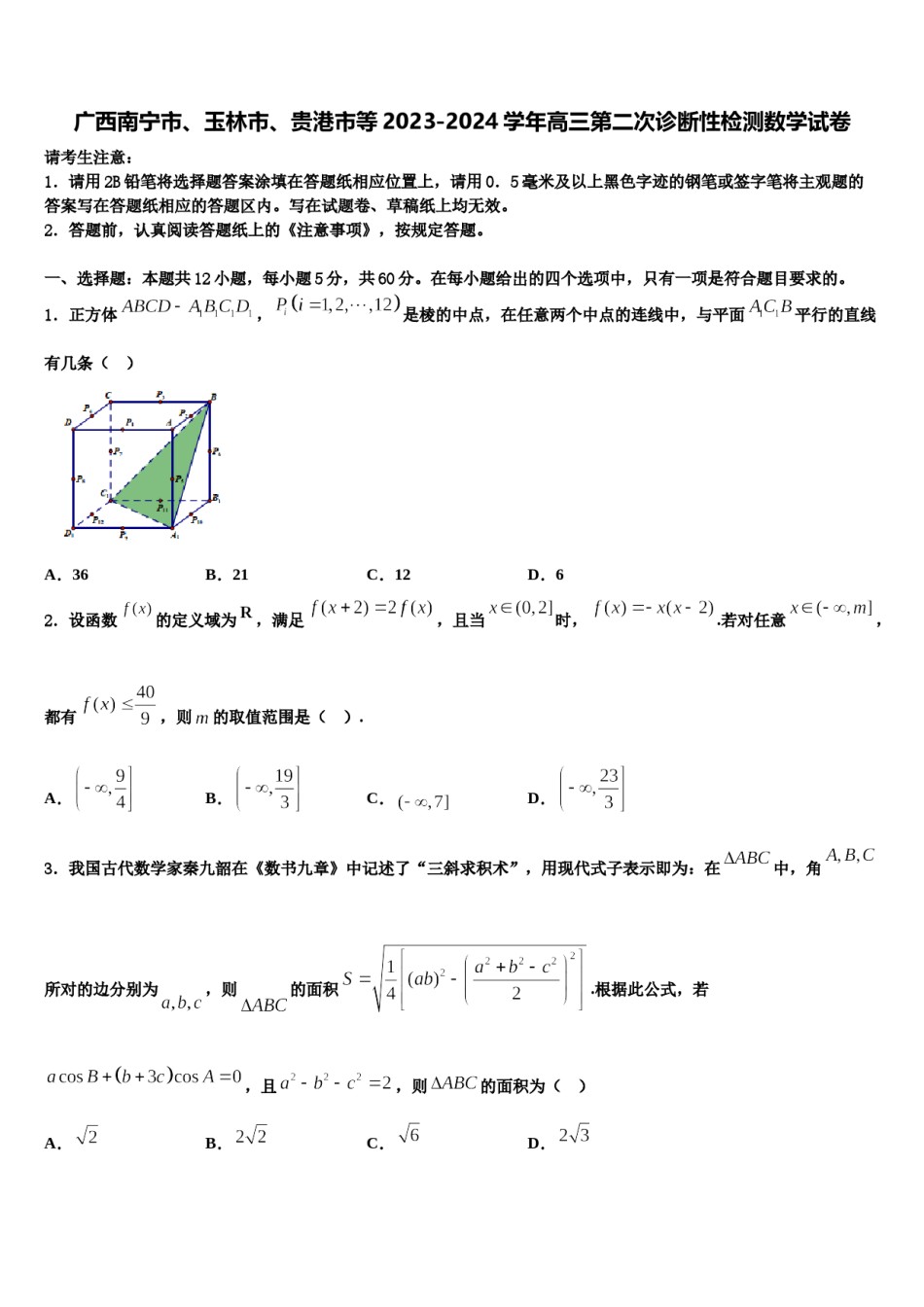
广西南宁市、玉林市、贵港市等2023-2024学年高三第二次诊断性检测数学试卷请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.正方体,是棱的中点,在任意两个中点的连线中,与平面平行的直线有几条()A.36B.21C.12D.6.若对任意,2.设函数的定义域为,满足,且当时,都有,则的取值范围是().A.B.C.D.3.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在中,角所对的边分别为,则的面积.根据此公式,若,且,则的面积为()A.B.C.D.4.已知数列是公比为的等比数列,且,若数列是递增数列,则的取值范围为()A.B.C.D.5.某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是()A.B.C.16D.326.如图,平面与平面相交于,,,点,点,则下列叙述错误的是()A.直线与异面,若对,B.过只有唯一平面与平行C.过点只能作唯一平面与垂直D.过一定能作一平面与垂直7.已知函数是奇函数,且恒成立,则的取值范围是()A.B.C.D.8.已知m为实数,直线:,:,则“”是“”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件9.已知,则不等式的解集是()A.B.C.D.10.若、满足约束条件,则的最大值为()A.B.C.D.11.复数为纯虚数,则()A.iC.2i12.已知集合B.﹣2iD.﹣i,,,则()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.某种产品的质量指标值服从正态分布,且.某用户购买了件这种产品,则这件产品中质量指标值位于区间之外的产品件数为_________.14.若函数,则__________;__________.15.如果抛物线上一点到准线的距离是6,那么______.16.设为数列的前项和,若,则____三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知数列的前项和为,.(1)求数列的通项公式;(2)若,为数列的前项和.求证:.18.(12分)已知椭圆:,不与坐标轴垂直的直线与椭圆交于,两点.(Ⅰ)若线段的中点坐标为,求直线的方程;(Ⅱ)若直线过点,点满足(,分别为直线,的斜率),求的值.19.(12分)如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,,交于点.求证:~.20.(12分)在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)把的参数方程化为极坐标方程:(2)求与交点的极坐标.21.(12分)如图,四棱锥V﹣ABCD中,底面ABCD是菱形,对角线AC与BD交于点O,VO⊥平面ABCD,E是棱VC的中点.(1)求证:VA∥平面BDE;(2)求证:平面VAC⊥平面BDE.22.(10分)如图,空间几何体中,是边长为2的等边三角形,,,,平面平面,且平面平面,为中点.(1)证明:平面;(2)求二面角平面角的余弦值.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】先找到与平面平行的平面,利用面面平行的定义即可得到.【详解】考虑与平面平行的平面,平面,平面,共有,故选:B.【点睛】本题考查线面平行的判定定理以及面面平行的定义,涉及到了简单的组合问题,是一中档题.2、B【解析】求出在的解析式,作出函数图象,数形结合即可得到答案.【详解】当时,,,,,又,所以至少小于7,此时令,得,解得或,结合图象,故.故选:B.【点睛】本题考查不等式恒成立求参数的范围,考查学生数形结合的思想,是一道中档题.3、A【解析】根据,利用正弦定理边化为角得,整理为,根据,得,再由余弦定理得,又,代入公式【详解】求解.,由,即得,即因为,所以,由余弦定理,所以,由的面积公式得故选:A【点睛】本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于...