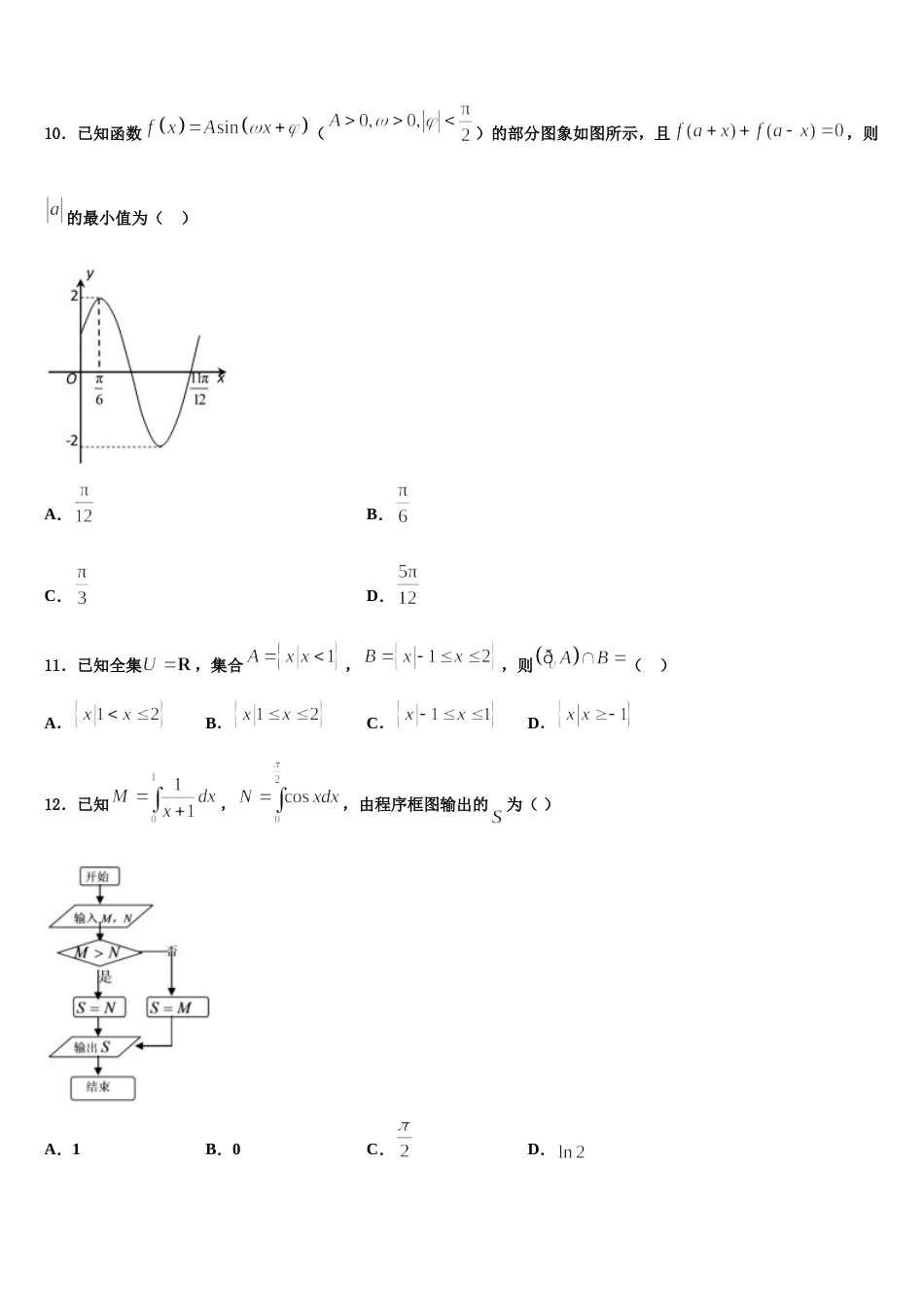
广西南宁第二中学 2024 年高考仿真卷数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.设复数满足,在复平面内对应的点为,则( )A.B.C.D.3.如图所示是某年第一季度五省 GDP 情况图,则下列说法中不正确的是( )A.该年第一季度 GDP 增速由高到低排位第 3 的是山东省B.与去年同期相比,该年第一季度的 GDP 总量实现了增长C.该年第一季度 GDP 总量和增速由高到低排位均居同一位的省份有 2 个D.去年同期浙江省的 GDP 总量超过了 4500 亿元4.在边长为 1 的等边三角形中,点 E 是中点,点 F 是中点,则( )A.B.C.D.5.已知函数在区间上恰有四个不同的零点,则实数的取值范围是( )A.B.C.D.6.若为纯虚数,则 z=( )A.B.6iC.D.207.如图,四面体中,面和面都是等腰直角三角形,,,且二面角的大小为,若四面体的顶点都在球上,则球的表面积为( )A.B.C.D.8.下列函数中,在区间上为减函数的是( )A.B.C.D.9.已知水平放置的△ABC 是按“斜二测画法”得到如图所示的直观图,其中 B′O′=C′O′=1,A′O′=,那么原△ABC 的面积是( )A.B.2C.D.10.已知函数()的部分图象如图所示,且,则的最小值为( )A.B.C.D.11.已知全集,集合,,则( )A.B.C.D.12.已知,,由程序框图输出的为( )A.1B.0C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知平面向量与的夹角为,,,则________.14.如图,在长方体中,,E,F,G 分别为的中点,点 P在平面 ABCD 内,若直线平面 EFG,则线段长度的最小值是________________.15.已知在等差数列中,,,前 n 项和为,则________.16.已知函数,则过原点且与曲线相切的直线方程为____________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)设函数.( )Ⅰ 当时,求不等式的解集;()Ⅱ 若函数 的图象与直线所围成的四边形面积大于 20,求的取值范围.18.(12 分)如图,在直三棱柱中,,点 P,Q 分别为,的中点.求证:(1)PQ平面;(2)平面.19.(12 分)如图所示,在四棱锥中,平面,底面 ABCD 满足 AD∥BC,,,E 为 AD 的中点,AC 与 BE 的交点为 O.(1)设 H 是线段 BE 上的动点,证明:三棱锥的体积是定值;(2)求四棱锥的体积;(3)求直线 BC 与平面 PBD 所成角的余弦值.20.(12 分)已知椭圆:的离心率为,直线 :与以原点为圆心,以椭圆的短半轴长为半径的圆相切.为左顶点,过点的直线交椭圆于,两点,直线,分别交直线于,两点.(1)求椭圆的方程;(2)以线段为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.21.(12 分)一个工厂在某年里连续 10 个月每月产品的总成本(万元)与该月产量(万件)之间有如下一组数据:1.081.121.191.281.361.481.591.681.801.872.252.372.402.552.642.752.923.033.143.26(1)通过画散点图,发现可用线性回归模型拟合与的关系,请用相关系数加以说明;(2)①建立月总成本与月产量之间的回归方程;②通过建立的关于的回归方程,估计某月产量为 1.98 万件时,产品的总成本为多少万元?(均精确到 0.001)附注:①参考数据:,,,,.② 参考公式:相关系数,,.22.(10 分)设直线 与抛物线交于两点,与椭圆交于两点,设直线(为坐标原点)的斜率分别为,若.(1)证明:直线 过定点,并求出该定点的坐标;(2)是否存在常数,满足?并说明理由.参考答案一、选择题:本题共 12 小题,每...