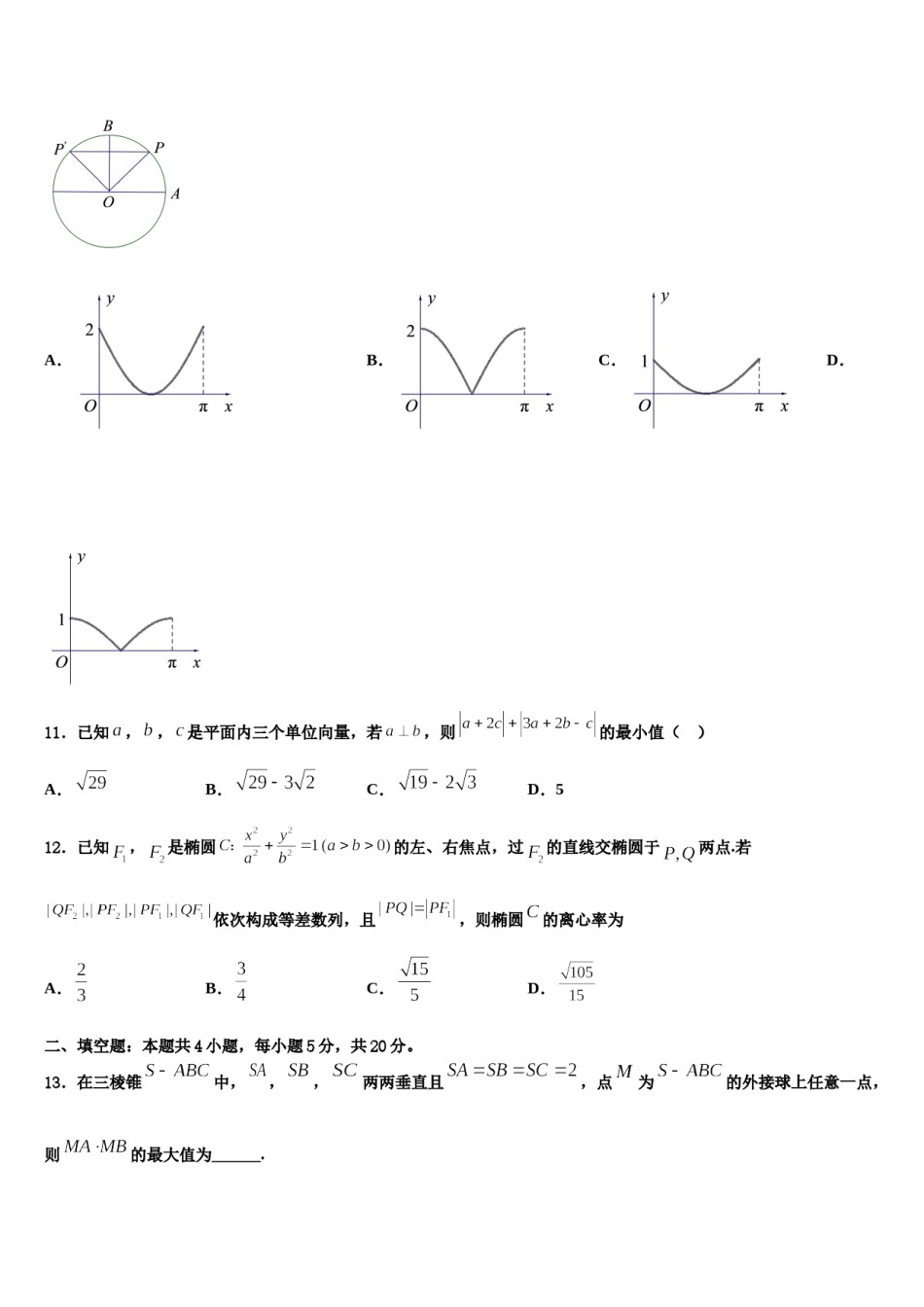
广西柳州二中2024年高考压轴卷数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知数列的通项公式是,则()A.0B.55C.66D.782.已知i是虚数单位,则()A.B.C.D.3.已知,则()A.B.C.D.4.在等差数列中,若,则()A.85.若函数B.12C.14D.10恰有3个零点,则实数的取值范围是()A.B.C.D.6.已知抛物线和点,直线与抛物线交于不同两点,,直线与抛物线交于另一点.给出以下判断:①以为直径的圆与抛物线准线相离;②直线与直线的斜率乘积为;③设过点,,的圆的圆心坐标为,半径为,则.C.②③D.①②③其中,所有正确判断的序号是()A.①②B.①③7.已知复数满足,则=()A.B.C.D.8.若实数、满足,则的最小值是()A.B.C.D.9.从装有除颜色外完全相同的3个白球和个黑球的布袋中随机摸取一球,有放回的摸取5次,设摸得白球数为,已知,则A.B.C.D.10.如图,圆的半径为,,是圆上的定点,,是圆上的动点,点关于直线的对称点为,角的始边为射线,终边为射线,将表示为的函数,则在上的图像大致为()A.B.C.D.11.已知,,是平面内三个单位向量,若,则的最小值()A.B.C.D.512.已知,是椭圆的左、右焦点,过的直线交椭圆于两点.若依次构成等差数列,且,则椭圆的离心率为A.B.C.D.,点为二、填空题:本题共4小题,每小题5分,共20分。13.在三棱锥中,,,两两垂直且的外接球上任意一点,则的最大值为______.14.已知关于x的不等式(ax﹣a2﹣4)(x﹣4)>0的解集为A,且A中共含有n个整数,则当n最小时实数a的值为_____.15.若奇函数满足,为R上的单调函数,对任意实数都有,当时,,则________.16.如图是九位评委打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均分为_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数(1)讨论的单调性;(2)当时,,求的取值范围.18.(12分)在中,角,,所对的边分别是,,,且.,其中(1)求的值;(2)若,求的取值范围.19.(12分)在平面直角坐标系中,已知向量,.(1)求的值;(2)若,且,求的值.20.(12分)已知四棱锥中,底面为等腰梯形,,,,丄底面.(1)证明:平面平面;(2)过的平面交于点,若平面把四棱锥分成体积相等的两部分,求二面角的余弦值.21.(12分)已知椭圆的焦距为,斜率为的直线与椭圆交于两点,若线段的中点为,且直线的斜率为.(1)求椭圆的方程;(2)若过左焦点斜率为的直线与椭圆交于点为椭圆上一点,且满足,问:是否为定值?若是,求出此定值,若不是,说明理由.22.(10分)已知.(1)当时,求不等式的解集;(2)若时不等式成立,求的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】先分为奇数和偶数两种情况计算出的值,可进一步得到数列的通项公式,然后代入转化计算,再根据等差数列求和公式计算出结果.【详解】解:由题意得,当为奇数时,,当为偶数时,;当为偶数时,,所以当为奇数时,所以故选:D【点睛】此题考查数列与三角函数的综合问题,以及数列求和,考查了正弦函数的性质应用,等差数列的求和公式,属于中档题.2、D【解析】利用复数的运算法则即可化简得出结果【详解】故选【点睛】本题考查了复数代数形式的乘除运算,属于基础题。3、B【解析】利用诱导公式以及同角三角函数基本关系式化简求解即可.【详解】,本题正确选项:【点睛】本题考查诱导公式的应用,同角三角函数基本关系式的应用,考查计算能力.4、C【解析】将,分别用和的形式表示,然后求解出和的值即可表示.【详解】设等差数列的首项为,公差为,则...