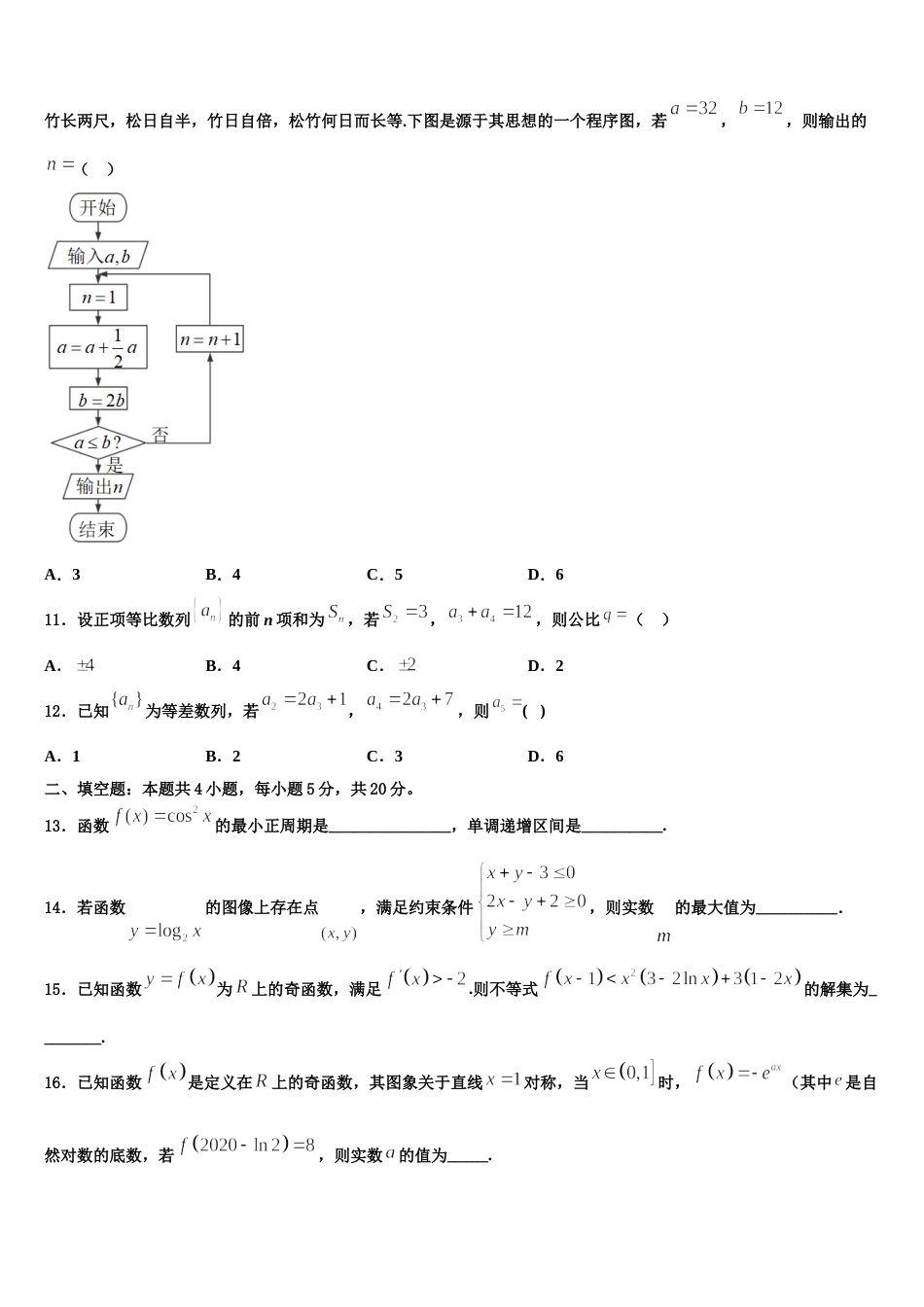
广西梧州柳州 2024 届高三第二次联考数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设,,则“”是“”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件2.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍.其中记载有求“囷盖”的术:“置如其周,令相承也.又以高乘之,三十六成一”.该术相当于给出了由圆锥的底面周长与高,计算其体积的近似公式.它实际上是将圆锥体积公式中的圆周率近似取为 3.那么近似公式相当于将圆锥体积公式中的圆周率近似取为( )A.B.C.D.3.如图所示,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则该几何体的体积是( )A.B.C.D.84.若(1+2ai)i=1-bi,其中 a,bR∈ ,则|a+bi|=( ).A.B.C.D.55.著名的斐波那契数列:1,1,2,3,5,8,…,满足,,,若,则( )A.2020B.4038C.4039D.40406.二项式的展开式中,常数项为( )A.B.80C.D.1607.如图所示的程序框图,若输入,,则输出的结果是( )A.B.C.D.8.设复数满足,在复平面内对应的点的坐标为则( )A.B.C.D.9.定义,已知函数,,则函数的最小值为( )A.B.C.D.10.元代数学家朱世杰的数学名著《算术启蒙》是中国古代代数学的通论,其中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.下图是源于其思想的一个程序图,若,,则输出的( )A.3B.4C.5D.611.设正项等比数列的前 n 项和为,若,,则公比( )A.B.4C.D.212.已知为等差数列,若,,则( )A.1B.2C.3D.6二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.函数的最小正周期是_______________,单调递增区间是__________.14.若函数的图像上存在点,满足约束条件,则实数的最大值为__________.15.已知函数为上的奇函数,满足.则不等式的解集为________.16.已知函数是定义在上的奇函数,其图象关于直线对称,当时,(其中 是自然对数的底数,若,则实数的值为_____.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数,且.(1)求的解析式;(2)已知,若对任意的,总存在,使得成立,求的取值范围.18.(12 分)已知等比数列是递增数列,且.(1)求数列的通项公式;(2)若,求数列的前项和.19.(12 分)在平面直角坐标系中,已知椭圆:()的左、右焦点分别为、,且点、与椭圆的上顶点构成边长为 2 的等边三角形.(1)求椭圆的方程;(2)已知直线 与椭圆相切于点,且分别与直线和直线相交于点、.试判断是否为定值,并说明理由.20.(12 分)设函数 f(x)=x2−4xsinx−4cosx. (1)讨论函数 f(x)在[−π,π]上的单调性;(2)证明:函数 f(x)在 R 上有且仅有两个零点.21.(12 分)已知,均为正数,且.证明:(1);(2).22.(10 分)已知直线 l 的极坐标方程为,圆 C 的参数方程为(为参数).(1)请分别把直线 l 和圆 C 的方程化为直角坐标方程;(2)求直线 l 被圆截得的弦长.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据对数的运算分别从充分性和必要性去证明即可.【详解】若, ,则,可得;若,可得,无法得到,所以“”是“”的充分而不必要条件.所以本题答案为 A.【点睛】本题考查充要条件的定义,判断充要条件的方法是:① 若为真命题且为假命题,则命题 p 是命题 q 的充分不必要条件;② 若为假命题且为真命题,则命题 p 是命题 q 的必要...