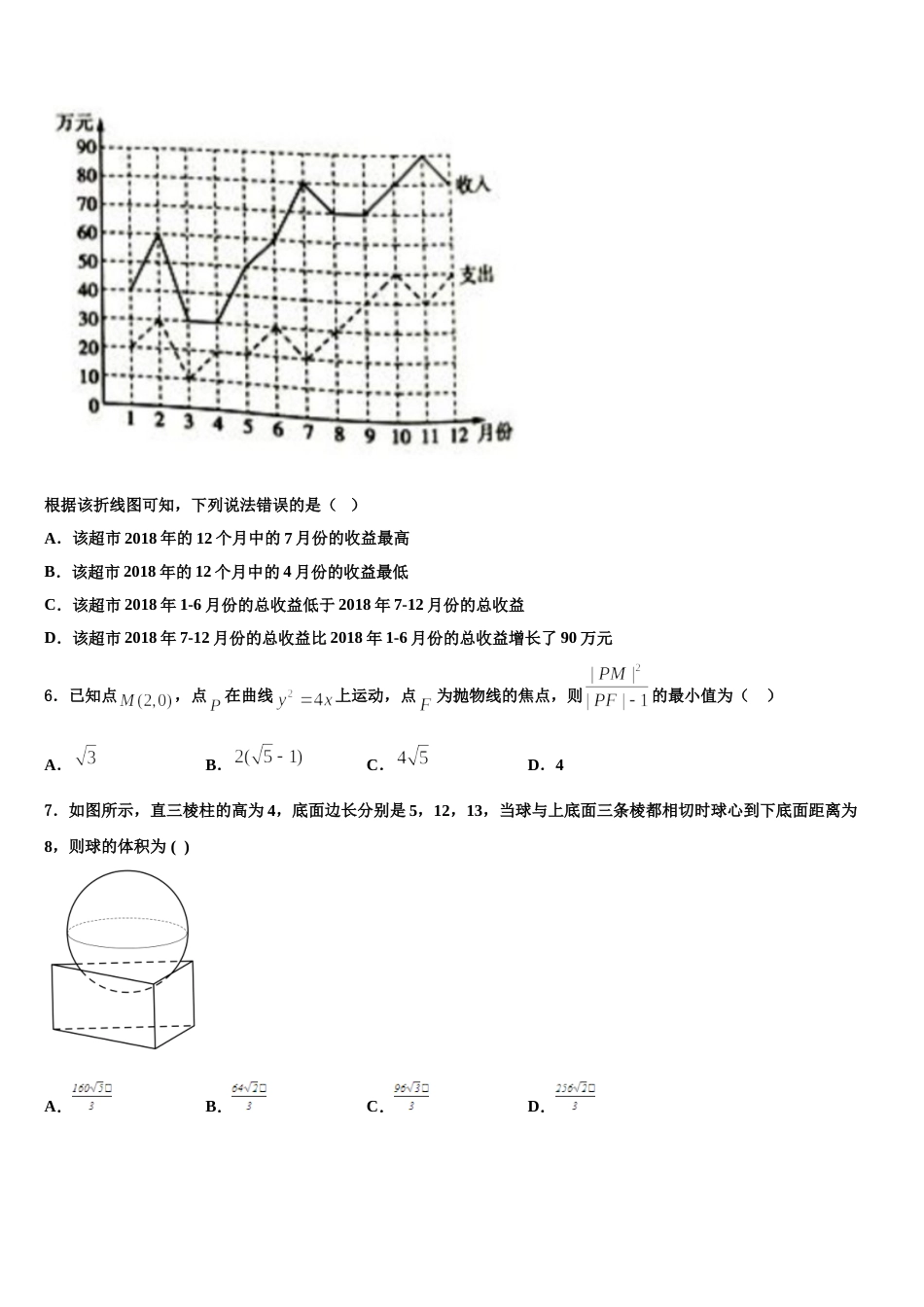
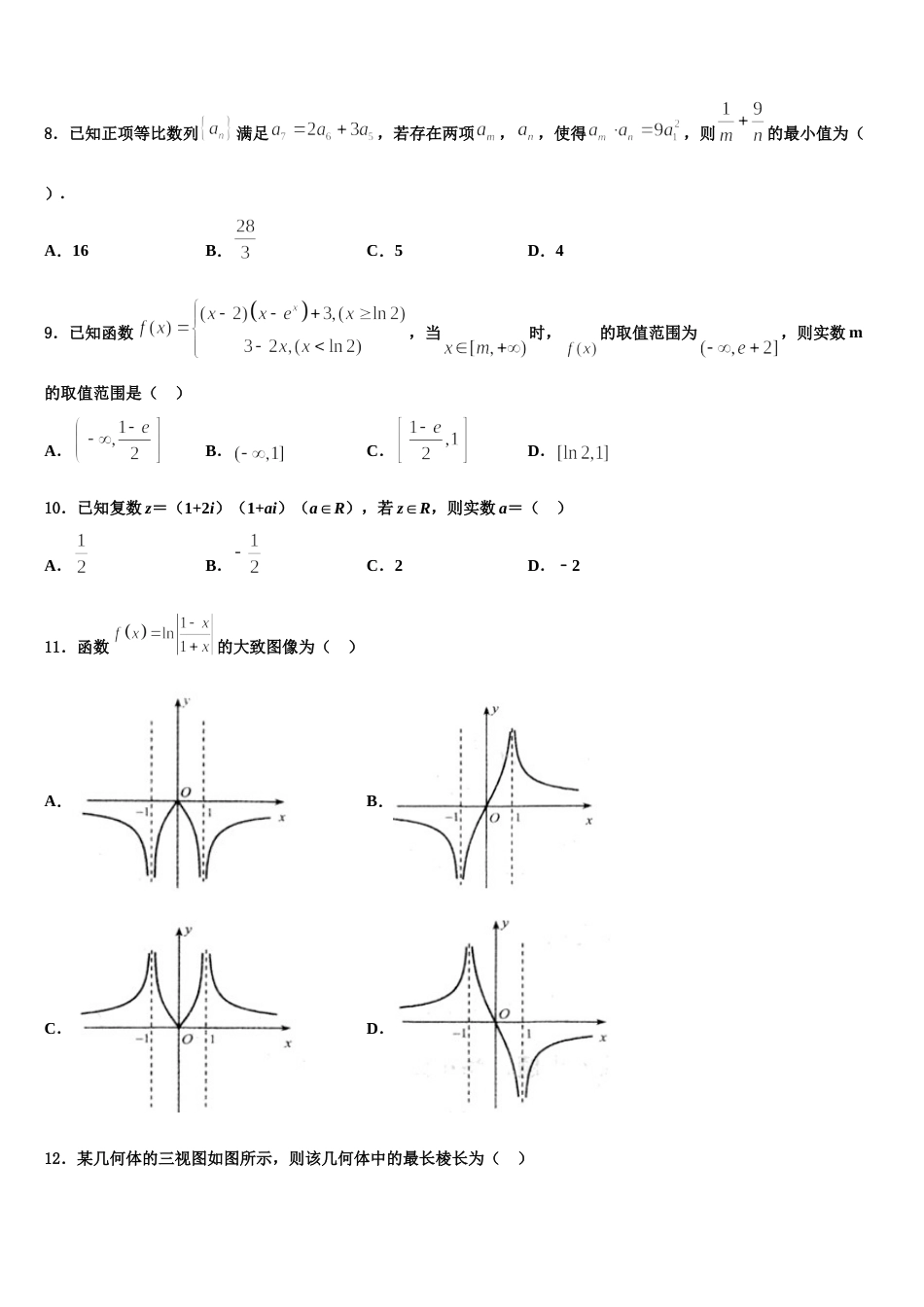
广西省贵港市 2024 届高三第三次模拟考试数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知 为虚数单位,复数满足,则复数在复平面内对应的点在( )A.第一象限B.第二象限C.第三象限D.第四象限2.我国古代数学巨著《九章算术》中,有如下问题:“今有女子善织,日自倍,五日织五尺,问日织几何?”这个问题用今天的白话叙述为:有一位善于织布的女子,每天织的布都是前一天的 2 倍,已知她 5 天共织布 5 尺,问这位女子每天分别织布多少?根据上述问题的已知条件,若该女子共织布尺,则这位女子织布的天数是( )A.2B.3C.4D.13.已知双曲线的离心率为 ,抛物线的焦点坐标为,若,则双曲线的渐近线方程为( )A.B.C.D.4.已知函数,,若成立,则的最小值是( )A.B.C.D.5.已知某超市 2018 年 12 个月的收入与支出数据的折线图如图所示:根据该折线图可知,下列说法错误的是( )A.该超市 2018 年的 12 个月中的 7 月份的收益最高B.该超市 2018 年的 12 个月中的 4 月份的收益最低C.该超市 2018 年 1-6 月份的总收益低于 2018 年 7-12 月份的总收益D.该超市 2018 年 7-12 月份的总收益比 2018 年 1-6 月份的总收益增长了 90 万元6.已知点,点在曲线上运动,点为抛物线的焦点,则的最小值为( )A.B.C.D.47.如图所示,直三棱柱的高为 4,底面边长分别是 5,12,13,当球与上底面三条棱都相切时球心到下底面距离为8,则球的体积为 ( ) A.B.C.D.8.已知正项等比数列满足,若存在两项,,使得,则的最小值为( ).A.16B.C.5D.49.已知函数,当时,的取值范围为,则实数 m的取值范围是( )A.B.C.D.10.已知复数 z=(1+2i)(1+ai)(a∈R),若 z∈R,则实数 a=( )A.B.C.2D.﹣211.函数的大致图像为( )A.B.C.D.12.某几何体的三视图如图所示,则该几何体中的最长棱长为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.设双曲线的左焦点为,过点且倾斜角为 45°的直线与双曲线的两条渐近线顺次交于,两点若,则的离心率为________.14.在中,已知,则的最小值是________.15.若函数为奇函数,则_______.16.已知实数满足则的最大值为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,已知正方形所在平面与梯形所在平面垂直,BM∥AN,,,.(1)证明:平面;(2)求点 N 到平面 CDM 的距离.18.(12 分)如图,在四棱锥中,平面,,为的中点.(1)求证:平面;(2)求二面角的余弦值.19.(12 分)已知椭圆与 x 轴负半轴交于,离心率.(1)求椭圆 C 的方程;(2)设直线与椭圆 C 交于两点,连接 AM,AN 并延长交直线 x=4 于两点,若,直线 MN 是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.20.(12 分)已知函数.(1)当时,求曲线在点处的切线方程;(2)若在上恒成立,求的取值范围.21.(12 分)某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数与烧开一壶水所用时间的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).表中,.(1)根据散点图判断,与哪一个更适宜作烧水时间关于开关旋钮旋转的弧度数的回归方程类型?(不必说明理由)(2)根据判断结果和表中数据,建立关于的回归方程;(3)若单位时间内煤气输出量 与旋转的弧度数成正比,那么,利用第(2)问求得的回归方程知为多少时,烧开一壶水最省煤气?附:对于一组数据,其回归直线的斜率和截距的最小二乘法估计值分别...