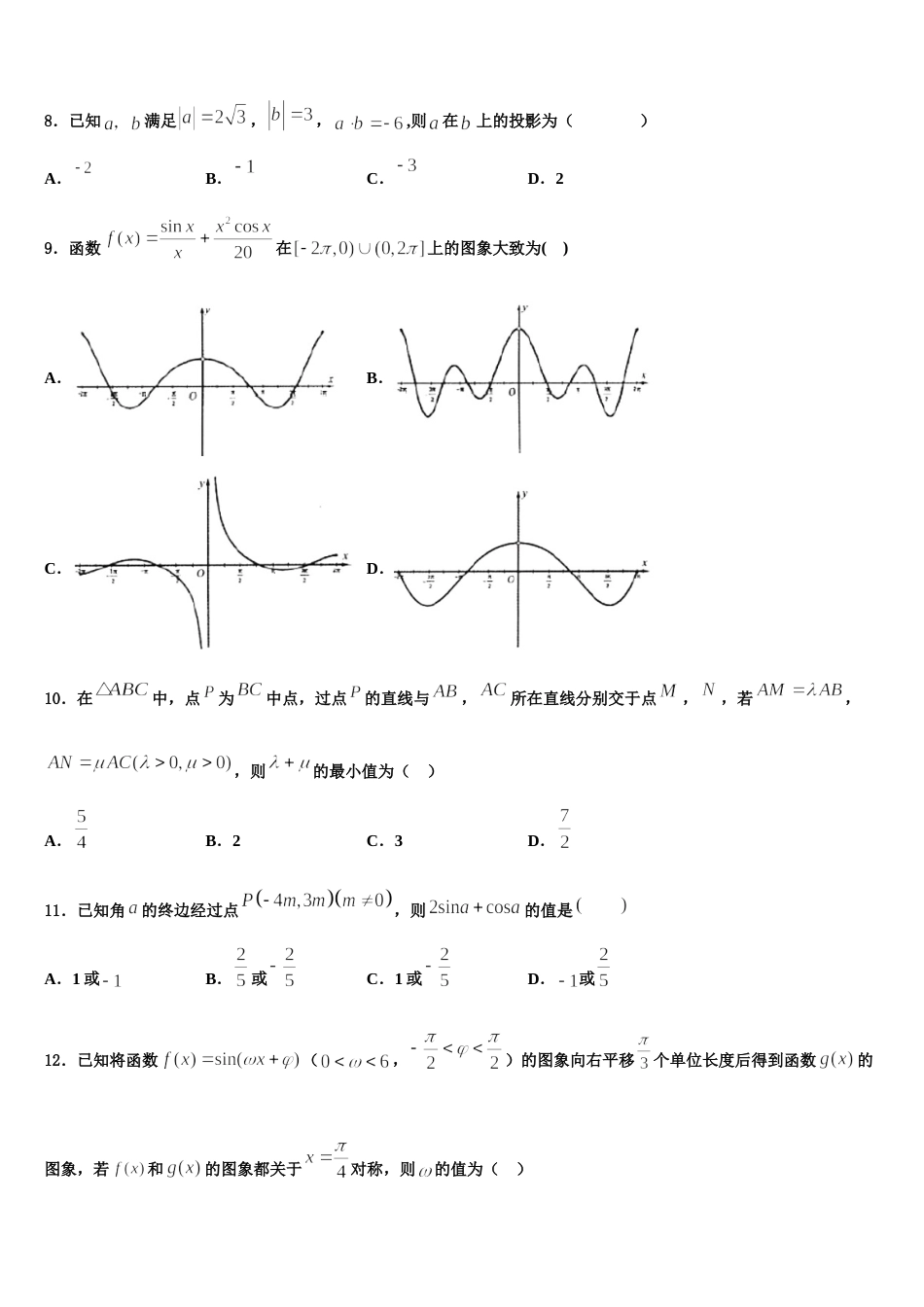
杭州市采荷中学 2024 年高考数学二模试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用 2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的部分图象大致为( )A.B.C.D.2.已知抛物线:的焦点为,准线为 ,是 上一点,直线与抛物线交于,两点,若,则为( )A.B.40C.16D.3.《易经》包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深,对今天 的几何学和其它学科仍有深刻的影响.下图就是易经中记载的几何图形——八卦田,图中正八 边形代表八卦,中间的圆代表阴阳太极图,八块面积相等的曲边梯形代表八卦田.已知正八边 形的边长为,阴阳太极图的半径为,则每块八卦田的面积约为( )A.B.C.D.4.已知数列的前 n 项和为,,且对于任意,满足,则( )A.B.C.D.5.若函数(其中,图象的一个对称中心为,,其相邻一条对称轴方程为,该对称轴处所对应的函数值为,为了得到的图象,则只要将的图象( )A.向右平移个单位长度B.向左平移个单位长度C.向左平移个单位长度D.向右平移个单位长度6.已知函数,若关于的方程有 4 个不同的实数根,则实数的取值范围为( )A.B.C.D.7.记单调递增的等比数列的前项和为,若,,则( )A.B.C.D.8.已知满足,,,则在上的投影为( )A.B.C.D.29.函数在上的图象大致为( )A.B.C.D.10.在中,点为中点,过点的直线与,所在直线分别交于点,,若,,则的最小值为( )A.B.2C.3D.11.已知角的终边经过点,则的值是 A.1 或B.或C.1 或D.或12.已知将函数(,)的图象向右平移个单位长度后得到函数的图象,若和的图象都关于对称,则的值为( )A.2B.3C.4D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.如图,已知一块半径为 2 的残缺的半圆形材料,O 为半圆的圆心,,残缺部分位于过点 C 的竖直线的右侧,现要在这块材料上裁出一个直角三角形,若该直角三角形一条边在上,则裁出三角形面积的最大值为______.14.已知,满足约束条件,则的最小值为______.15.曲线在点处的切线方程为__.16. “今有女善织,日益功疾,初日织五尺,今一月共织九匹三丈.”其白话意译为:“现有一善织布的女子,从第2 天开始,每天比前一天多织相同数量的布,第一天织了 5 尺布,现在一个月(按 30 天计算)共织布 390 尺.”则每天增加的数量为____尺,设该女子一个月中第 n 天所织布的尺数为,则______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知,.(1)解;(2)若,证明:.18.(12 分)已知函数和的图象关于原点对称,且.(1)解关于的不等式;(2)如果对,不等式恒成立,求实数的取值范围.19.(12 分)某公园有一块边长为 3 百米的正三角形空地,拟将它分割成面积相等的三个区域,用来种植三种花卉.方案是:先建造一条直道将分成面积之比为的两部分(点 D,E 分别在边,上);再取的中点 M,建造直道(如图).设,,(单位:百米).(1)分别求,关于 x 的函数关系式;(2)试确定点 D 的位置,使两条直道的长度之和最小,并求出最小值.20.(12 分)如图,在四棱柱中,底面为菱形,.(1)证明:平面平面;(2)若,是等边三角形,求二面角的余弦值.21.(12 分)如图,已知三棱柱中,与是全等的等边三角形.(1)求证:;(2)若,求二面角的余弦值.22.(10 分)在直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,曲线的极坐标方程为.(1)求曲线的直角坐标方程和曲线的参数方程;(2)设曲线与曲线在第二象限的交点为,曲线与轴的交点为,点,求的周长 的最大值.参考答案一、选择题...