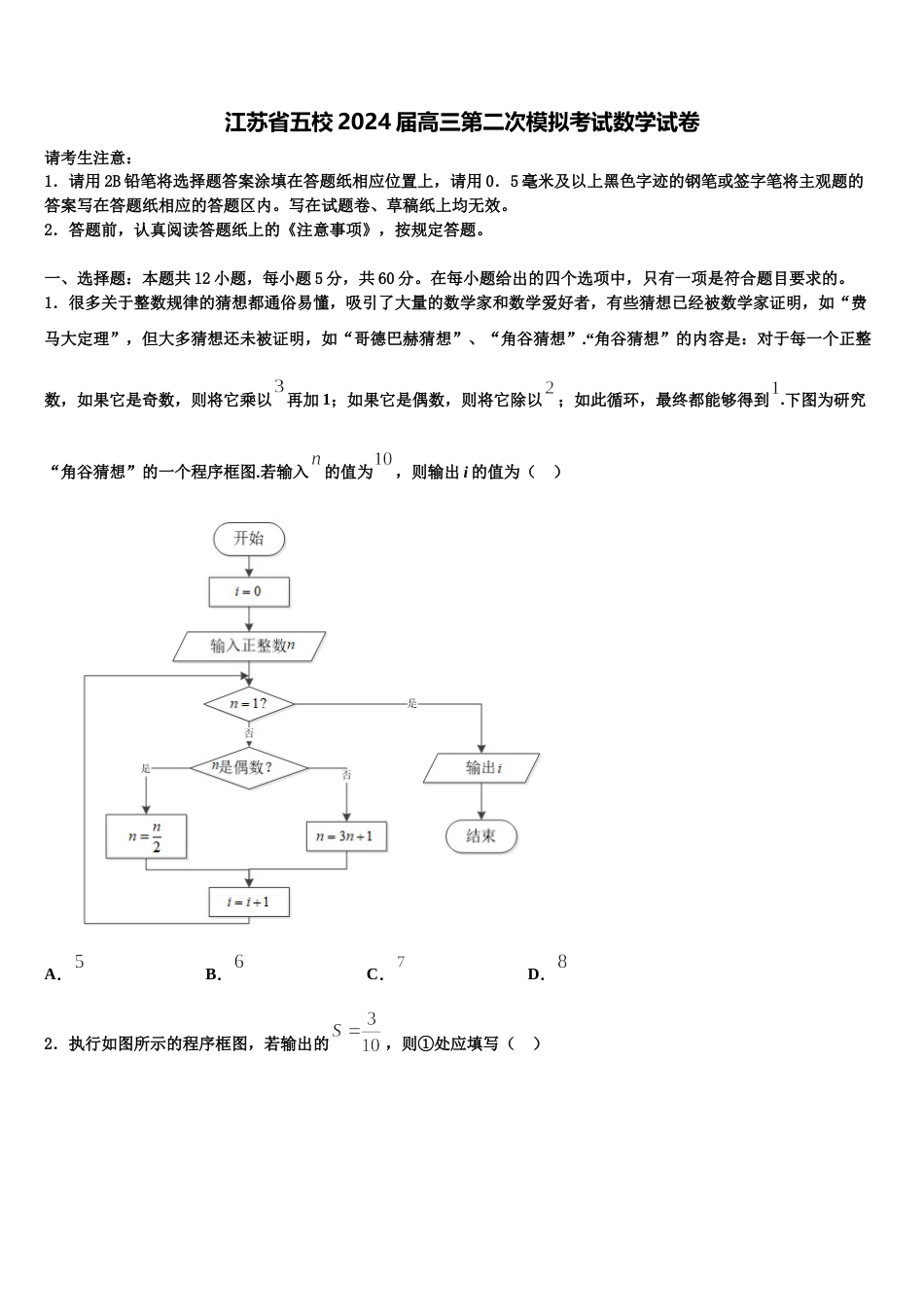
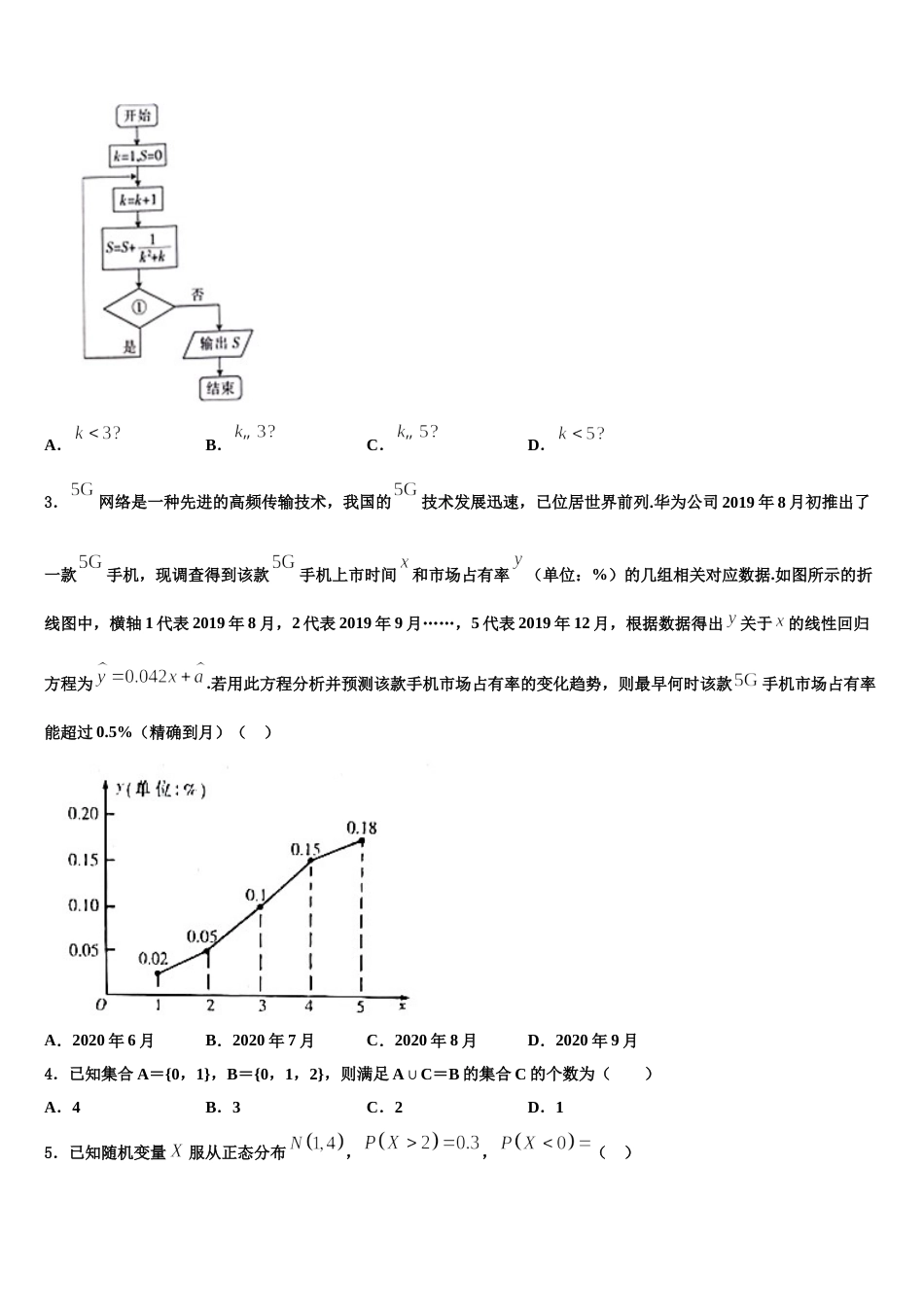
江苏省五校 2024 届高三第二次模拟考试数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以再加 1;如果它是偶数,则将它除以;如此循环,最终都能够得到 .下图为研究“角谷猜想”的一个程序框图.若输入的值为,则输出 i 的值为( )A.B.C.D.2.执行如图所示的程序框图,若输出的,则①处应填写( )A.B.C.D.3.网络是一种先进的高频传输技术,我国的技术发展迅速,已位居世界前列.华为公司 2019 年 8 月初推出了一款手机,现调查得到该款手机上市时间和市场占有率(单位:%)的几组相关对应数据.如图所示的折线图中,横轴 1 代表 2019 年 8 月,2 代表 2019 年 9 月……,5 代表 2019 年 12 月,根据数据得出关于的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势,则最早何时该款手机市场占有率能超过 0.5%(精确到月)( )A.2020 年 6 月B.2020 年 7 月C.2020 年 8 月D.2020 年 9 月4.已知集合 A={0,1},B={0,1,2},则满足 AC∪ =B 的集合 C 的个数为( )A.4B.3C.2D.15.已知随机变量服从正态分布,,( )A.B.C.D.6.已知角的顶点与坐标原点重合,始边与轴的非负半轴重合,它的终边过点,则的值为( )A.B.C.D.7.函数在上单调递增,则实数的取值范围是( )A.B.C.D.8.设集合,集合 ,则 =( )A.B.C.D.R9.在中,,,,为的外心,若,,,则( )A.B.C.D.10.设双曲线(,)的一条渐近线与抛物线有且只有一个公共点,且椭圆的焦距为 2,则双曲线的标准方程为( )A.B.C.D.11.已知变量,满足不等式组,则的最小值为( )A.B.C.D.12.已知定义在上的奇函数和偶函数满足(且),若,则函数的单调递增区间为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知正方形边长为,空间中的动点满足,,则三棱锥体积的最大值是______.14.已知函数是定义在上的奇函数,则的值为__________.15.已知实数 a,b,c 满足,则的最小值是______.16.若函数在区间上恰有 4 个不同的零点,则正数的取值范围是______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在平面直角坐标系中,曲线的参数方程为:(为参数),以为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为:.(1)求曲线的极坐标方程和曲线的直角坐标方程;(2)若直线与曲线交于,两点,与曲线交于,两点,求取得最大值时直线 的直角坐标方程.18.(12 分)如图,在四棱锥中,底面是直角梯形,,,,是正三角形,,是的中点.(1)证明:;(2)求直线与平面所成角的正弦值.19.(12 分)设数列的前列项和为,已知.(1)求数列的通项公式;(2)求证:.20.(12 分)已知.(1)当时,求不等式的解集;(2)若时不等式成立,求的取值范围.21.(12 分)已知,,函数的最小值为.(1)求证:;(2)若恒成立,求实数 的最大值.22.(10 分)己知等差数列的公差,,且,,成等比数列.(1)求使不等式成立的最大自然数 n;(2)记数列的前 n 项和为,求证:.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】根据程序框图列举出程序的每一步,即可得出输出结果.【详解】输入,不成立,是偶数成立,则,;不成立,是偶数不成立,则,;不...