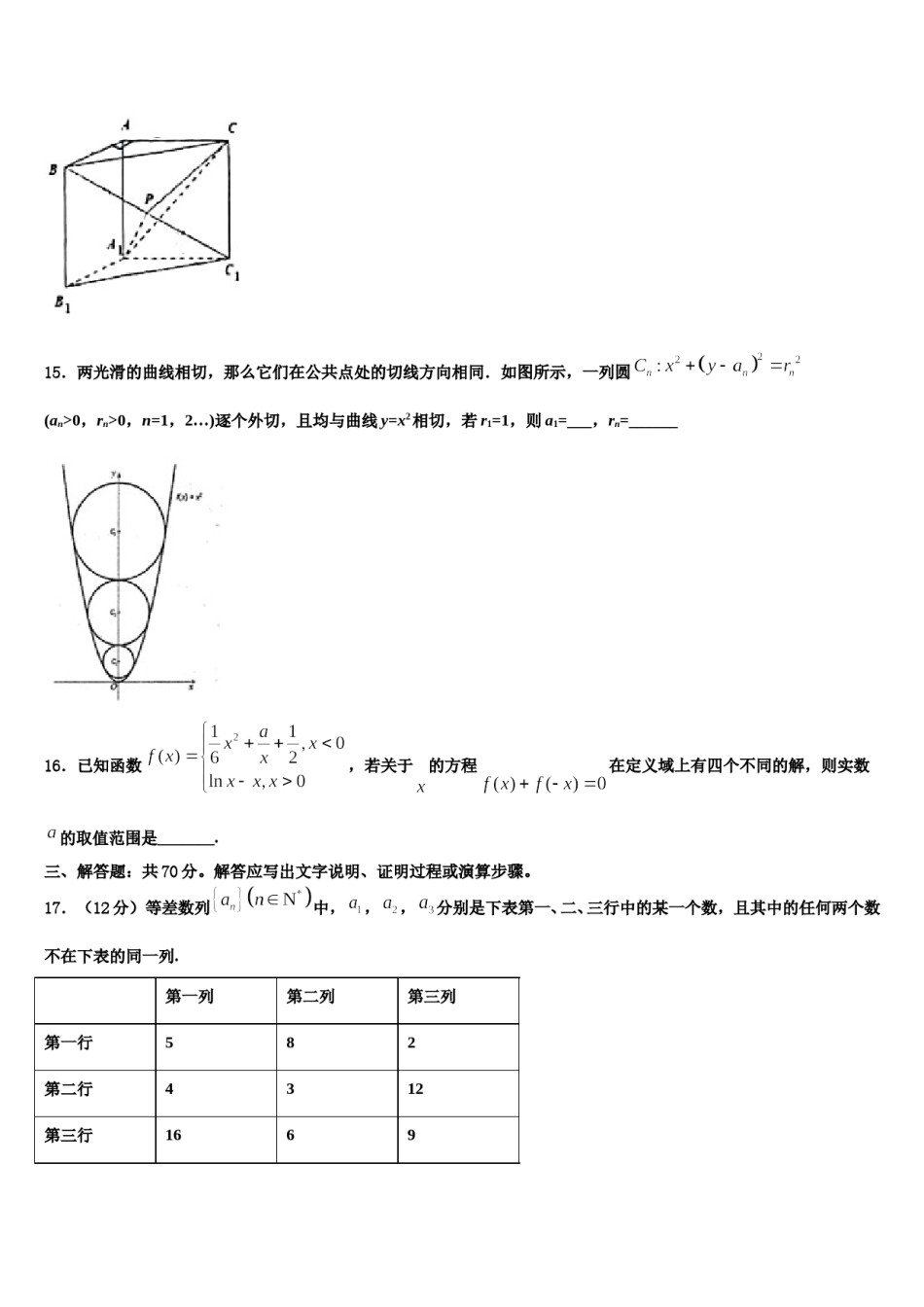
江苏省南通市包场中学2024年高考数学考前最后一卷预测卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知实数,,函数在上单调递增,则实数的取值范围是()A.B.C.D.2.已知集合等于()A.,,则3.若复数满足D.B.C.,则()A.B.C.D.4.设是两条不同的直线,是两个不同的平面,则下列命题正确的是()A.若,,则B.若,,则C.若,,,则D.若,,,则5.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案种数是()A.18种B.36种C.54种D.72种6.已知直线与圆有公共点,则的最大值为()A.4B.C.D.7.已知全集,集合,则=()A.B.的图象上一点,则线段的最小值为()C.D.8.已知与分别为函数与函数A.B.C.D.69.已知斜率为k的直线l与抛物线交于A,B两点,线段AB的中点为,则斜率k的取值范围是()A.B.C.D.10.已知是过抛物线焦点的弦,是原点,则()A.-2B.-4C.3D.-311.设等差数列的前n项和为,且,,则()A.9B.12C.D.12.函数的对称轴不可能为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知为正实数,且,则的最小值为____________.14.如图,直三棱柱中,,,,P是的中点,则三棱锥的体积为________.15.两光滑的曲线相切,那么它们在公共点处的切线方向相同.如图所示,一列圆(an>0,rn>0,n=1,2…)逐个外切,且均与曲线y=x2相切,若r1=1,则a1=___,rn=______16.已知函数,若关于的方程在定义域上有四个不同的解,则实数的取值范围是_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)等差数列中,,,分别是下表第一、二、三行中的某一个数,且其中的任何两个数不在下表的同一列.第二列第三列第一列第一行582第二行4312第三行1669(1)请选择一个可能的组合,并求数列的通项公式;(2)记(1)中您选择的的前项和为,判断是否存在正整数,使得,,成等比数列,若有,请求出的值;若没有,请说明理由.,分别是中点,且18.(12分)如图,在直三棱柱中,.求证:平面;求点到平面的距离.19.(12分)已知圆外有一点,过点作直线.(1)当直线与圆相切时,求直线的方程;(2)当直线的倾斜角为时,求直线被圆所截得的弦长.20.(12分)心形线是由一个圆上的一个定点,当该圆在绕着与其相切且半径相同的另外一个圆周上滚动时,这个定点的轨迹,因其形状像心形而得名,在极坐标系中,方程()表示的曲线就是一条心形线,如图,以极轴所在的直线为轴,极点为坐标原点的直角坐标系中.已知曲线的参数方程为(为参数).(1)求曲线的极坐标方程;(2)若曲线与相交于、、三点,求线段的长.21.(12分)已知是各项都为正数的数列,其前项和为,且为与的等差中项.(1)求证:数列为等差数列;(2)设,求的前100项和.22.(10分)设函数.(1)当时,求不等式的解集;(2)若恒成立,求的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】根据题意,对于函数分2段分析:当,由指数函数的性质分析可得①,当,由导数与函数单调性的关系可得,在上恒成立,变形可得②,再结合函数的单调性,分析可得③,联立三个式子,分析可得答案.【详解】解:根据题意,函数在上单调递增,当,若为增函数,则①,当,若为增函数,必有在上恒成立,变形可得:,又由,可得在上单调递减,则,若在上恒成立,则有②,若函数在上单调递增,左边一段函数的最大值不能大于右边一段函数的最小值,则需有,③联立①②③可得:.故选:D.【点睛】本题考查函数单调性的性质以及应用,注意分段函数单调性的性质.2、A【解析】进行交集的运算即可.【...