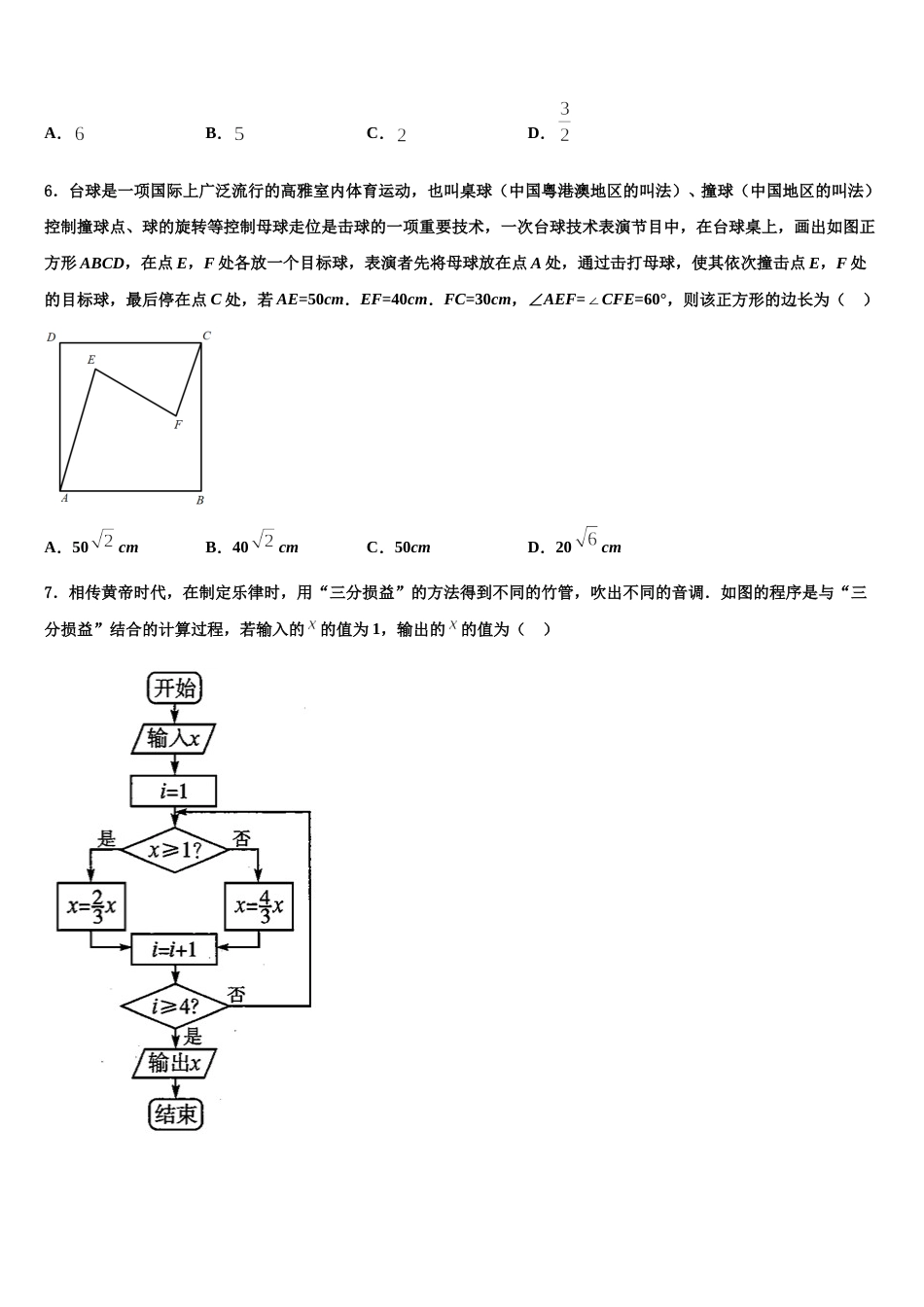
江苏省宿迁市沭阳县修远中学 2023-2024 学年高三(最后冲刺)数学试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.函数的图象可能是下面的图象( )A.B.C.D.2.设过点的直线分别与轴的正半轴和轴的正半轴交于两点,点与点关于轴对称,为坐标原点,若,且,则点的轨迹方程是( )A.B.C.D.3.已知函数是奇函数,则的值为( )A.-10B.-9C.-7D.14.曲线在点处的切线方程为( )A.B.C.D.5.若实数、满足,则的最小值是( )A.B.C.D.6.台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形 ABCD,在点 E,F 处各放一个目标球,表演者先将母球放在点 A 处,通过击打母球,使其依次撞击点 E,F 处的目标球,最后停在点 C 处,若 AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,则该正方形的边长为( )A.50cmB.40cmC.50cmD.20cm7.相传黄帝时代,在制定乐律时,用“三分损益”的方法得到不同的竹管,吹出不同的音调.如图的程序是与“三分损益”结合的计算过程,若输入的的值为 1,输出的的值为( )A.B.C.D.8.已知等差数列的公差不为零,且,,构成新的等差数列,为的前项和,若存在使得,则( )A.10B.11C.12D.139.设( 是虚数单位),则( )A.B.1C.2D.10.若是定义域为的奇函数,且,则A.的值域为B.为周期函数,且 6 为其一个周期C.的图像关于对称D.函数的零点有无穷多个11.若集合,,则( )A.B.C.D.12.在中,为边上的中点,且,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知,,是平面向量,是单位向量.若,,且,则的取值范围是________.14.如图,已知圆内接四边形 ABCD,其中,,,,则__________.15.成都市某次高三统考,成绩 X 经统计分析,近似服从正态分布,且,若该市有人参考,则估计成都市该次统考中成绩大于分的人数为_____.16.已知直线被圆截得的弦长为 2,则的值为__三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在底面为菱形的四棱柱中,平面.(1)证明:平面;(2)求二面角的正弦值.18.(12 分)如图,在三棱柱中,是边长为 2 的菱形,且,是矩形,,且平面平面,点在线段上移动(不与重合),是的中点.(1)当四面体的外接球的表面积为时,证明:.平面(2)当四面体的体积最大时,求平面与平面所成锐二面角的余弦值.19.(12 分)已知抛物线 Γ:y2=2px(p>0)的焦点为 F,P 是抛物线 Γ 上一点,且在第一象限,满足(2,2)(1)求抛物线 Γ 的方程;(2)已知经过点 A(3,﹣2)的直线交抛物线 Γ 于 M,N 两点,经过定点 B(3,﹣6)和 M 的直线与抛物线 Γ 交于另一点 L,问直线 NL 是否恒过定点,如果过定点,求出该定点,否则说明理由.20.(12 分)已知.(1)当时,求不等式的解集;(2)若,,证明:.21.(12 分)在四棱锥的底面是菱形, 底面,, 分别是的中点,.(Ⅰ)求证: ;(Ⅱ)求直线与平面所成角的正弦值;(III)在边上是否存在点,使与所成角的余弦值为,若存在,确定点的位置;若不存在,说明理由.22.(10 分)已知函数,.(1)若不等式对恒成立,求的最小值;(2)证明:.(3)设方程的实根为.令若存在,,,使得,证明:.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】因为,所以函数的图象关于点(2,0)对称,排除 A,B.当时,,所以,排除 D...