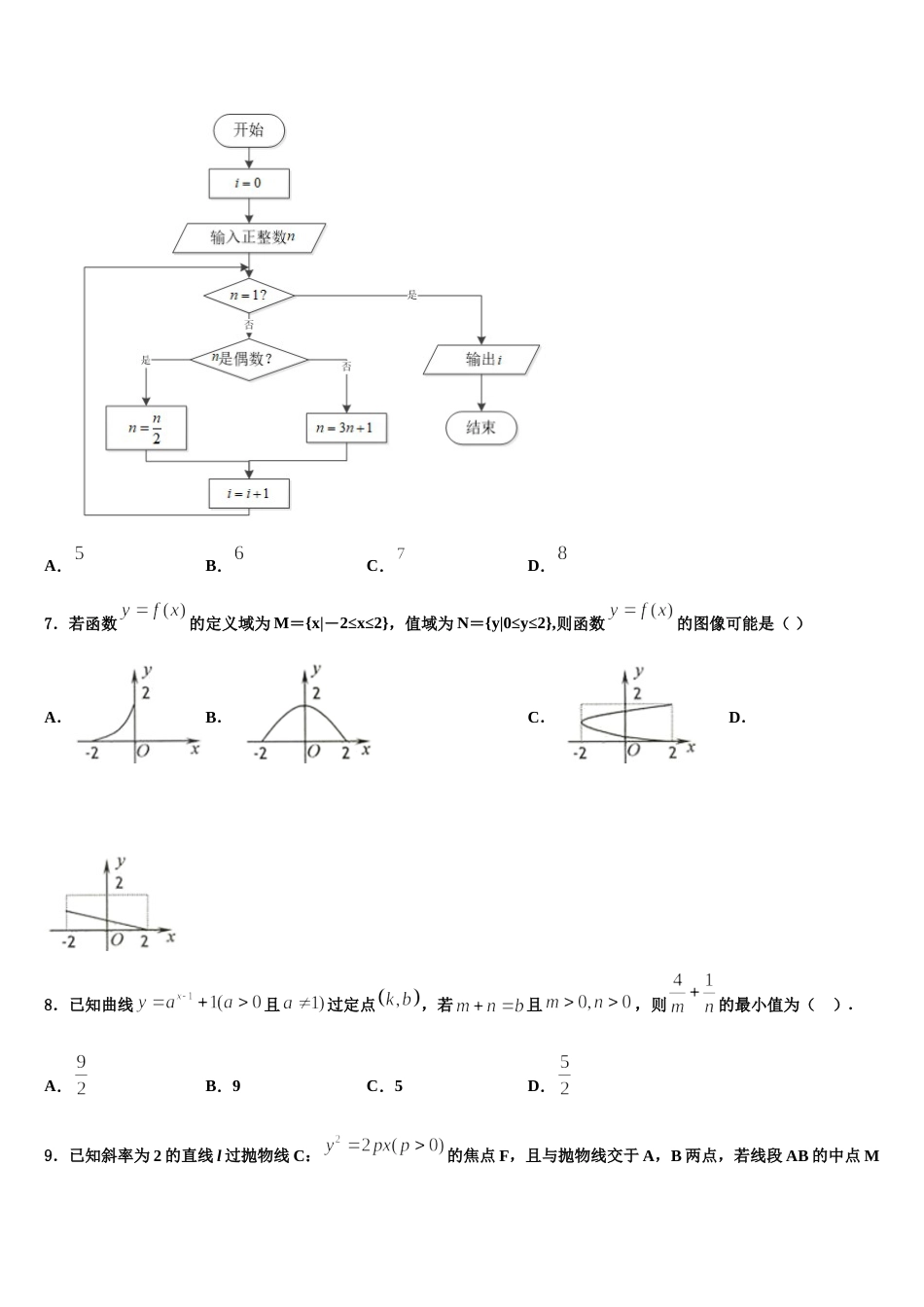
江苏省苏州新区实验中学 2024 年高考考前模拟数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设过点的直线分别与轴的正半轴和轴的正半轴交于两点,点与点关于轴对称,为坐标原点,若,且,则点的轨迹方程是( )A.B.C.D.2.如图,在直角梯形 ABCD 中,AB∥DC,AD⊥DC,AD=DC=2AB,E 为 AD 的中点,若,则 λ+μ 的值为( )A. B.C.D.3.已知命题:是“直线和直线互相垂直”的充要条件;命题:对任意都有零点;则下列命题为真命题的是( )A.B.C.D.4.某三棱锥的三视图如图所示,则该三棱锥的体积为( )A.B.4C.D.55.已知正项等比数列的前项和为,则的最小值为( )A.B.C.D.6.很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以再加 1;如果它是偶数,则将它除以;如此循环,最终都能够得到 .下图为研究“角谷猜想”的一个程序框图.若输入的值为,则输出 i 的值为( )A.B.C.D.7.若函数的定义域为 M={x|-2≤x≤2},值域为 N={y|0≤y≤2},则函数的图像可能是( )A.B.C.D.8.已知曲线且过定点,若且,则的最小值为( ).A.B.9C.5D.9.已知斜率为 2 的直线 l 过抛物线 C:的焦点 F,且与抛物线交于 A,B 两点,若线段 AB 的中点 M的纵坐标为 1,则 p=( )A.1B.C.2D.410.三棱柱中,底面边长和侧棱长都相等,,则异面直线与所成角的余弦值为( )A.B.C.D.11.已知,是两条不重合的直线,是一个平面,则下列命题中正确的是( )A.若,,则B.若,,则C.若,,则D.若,,则12.已知复数满足,则=( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知数列的前项和为,,且满足,则数列的前 10 项的和为______.14.若,则的最小值为________.15.在直角三角形中,为直角,,点在线段上,且,若,则的正切值为_____.16.设平面向量与的夹角为,且,,则的取值范围为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)第十三届全国人大常委会第十一次会议审议的《固体废物污染环境防治法(修订草案)》中,提出推行生活垃圾分类制度,这是生活垃圾分类首次被纳入国家立法中.为了解某城市居民的垃圾分类意识与政府相关法规宣传普及的关系,对某试点社区抽取户居民进行调查,得到如下的列联表.分类意识强分类意识弱合计试点后试点前合计已知在抽取的户居民中随机抽取 户,抽到分类意识强的概率为.(1)请将上面的列联表补充完整,并判断是否有的把握认为居民分类意识的强弱与政府宣传普及工作有关?说明你的理由;(2)已知在试点前分类意识强的户居民中,有户自觉垃圾分类在年以上,现在从试点前分类意识强的户居民中,随机选出户进行自觉垃圾分类年限的调查,记选出自觉垃圾分类年限在年以上的户数为,求分布列及数学期望.参考公式:,其中.下面的临界值表仅供参考18.(12 分)已知,且的解集为.(1)求实数,的值;(2)若的图像与直线及围成的四边形的面积不小于 14,求实数取值范围.19.(12 分)在四棱锥的底面中,,,平面,是的中点,且(Ⅰ)求证:平面;(Ⅱ)求二面角的余弦值;(Ⅲ...