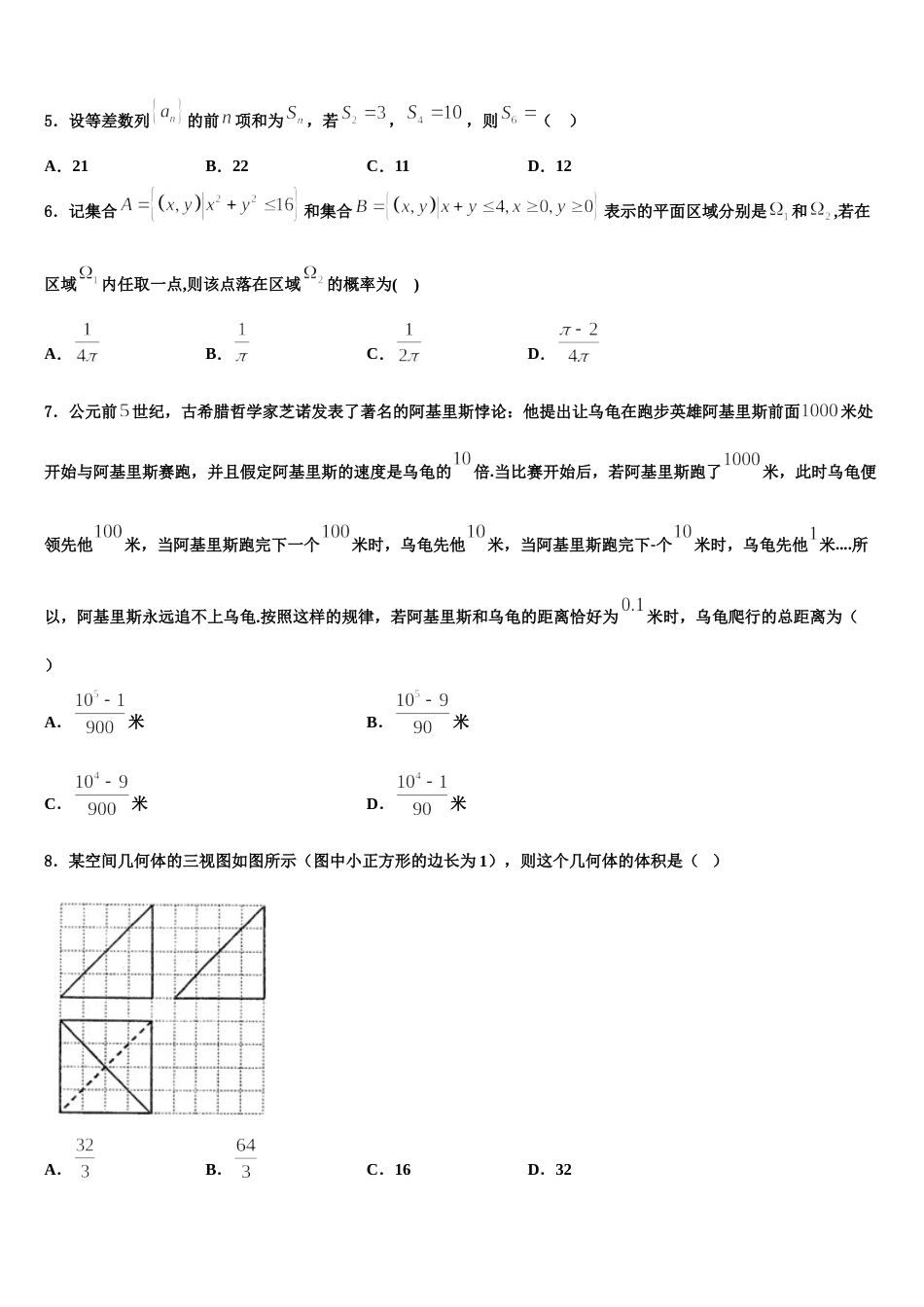
江苏省重点中学 2024 届高三 3 月份模拟考试数学试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用 2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用 05 毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用 2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知椭圆的右焦点为 F,左顶点为 A,点 P 椭圆上,且,若,则椭圆的离心率 为( )A.B.C.D.2.已知 f(x)=ax2+bx 是定义在[a–1,2a]上的偶函数,那么 a+b 的值是A.B.C.D.3.给定下列四个命题:① 若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行;② 若一个平面经过另一个平面的垂线,则这两个平面相互垂直;③ 垂直于同一直线的两条直线相互平行;④ 若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( )A.①和② B.②和③ C.③和④ D.②和④4.设不等式组表示的平面区域为,若从圆:的内部随机选取一点,则取自的概率为( )A.B.C.D.5.设等差数列的前项和为,若,,则( )A.21B.22C.11D.126.记集合和集合表示的平面区域分别是和,若在区域内任取一点,则该点落在区域的概率为( )A.B.C.D.7.公元前世纪,古希腊哲学家芝诺发表了著名的阿基里斯悖论:他提出让乌龟在跑步英雄阿基里斯前面米处开始与阿基里斯赛跑,并且假定阿基里斯的速度是乌龟的倍.当比赛开始后,若阿基里斯跑了米,此时乌龟便领先他米,当阿基里斯跑完下一个米时,乌龟先他米,当阿基里斯跑完下-个米时,乌龟先他 米....所以,阿基里斯永远追不上乌龟.按照这样的规律,若阿基里斯和乌龟的距离恰好为米时,乌龟爬行的总距离为( )A.米B.米C.米D.米8.某空间几何体的三视图如图所示(图中小正方形的边长为 1),则这个几何体的体积是( )A.B.C.16D.329.已知命题:是“直线和直线互相垂直”的充要条件;命题:对任意都有零点;则下列命题为真命题的是( )A.B.C.D.10.中国铁路总公司相关负责人表示,到 2018 年底,全国铁路营业里程达到 13.1 万公里,其中高铁营业里程 2.9 万公里,超过世界高铁总里程的三分之二,下图是 2014 年到 2018 年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )A.每相邻两年相比较,2014 年到 2015 年铁路运营里程增加最显著B.从 2014 年到 2018 年这 5 年,高铁运营里程与年价正相关C.2018 年高铁运营里程比 2014 年高铁运营里程增长 80%以上D.从 2014 年到 2018 年这 5 年,高铁运营里程数依次成等差数列11.在三角形中,,,求( )A.B.C.D.12.若 为虚数单位,则复数的共轭复数在复平面内对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若双曲线的两条渐近线斜率分别为,,若,则该双曲线的离心率为________.14.设,则除以的余数是______.15.二项式的展开式的各项系数之和为_____,含项的系数为_____.16.若函数,则__________;__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在三角形 ABC 中,角 A,B,C 的对边分别为 a,b,c,若,角为钝角, (1)求的值; (2)求边的长.18.(12 分)一种游戏的规则为抛掷一枚硬币,每次正面向上得 2 分,反面向上得 1 分.(1)设抛掷 4 次的得分为,求变量的分布列和数学期望.(2)当游戏得分为时,游戏停止,记得分的概率和为.① 求;② 当时,记,证明:数列为常数列,数...