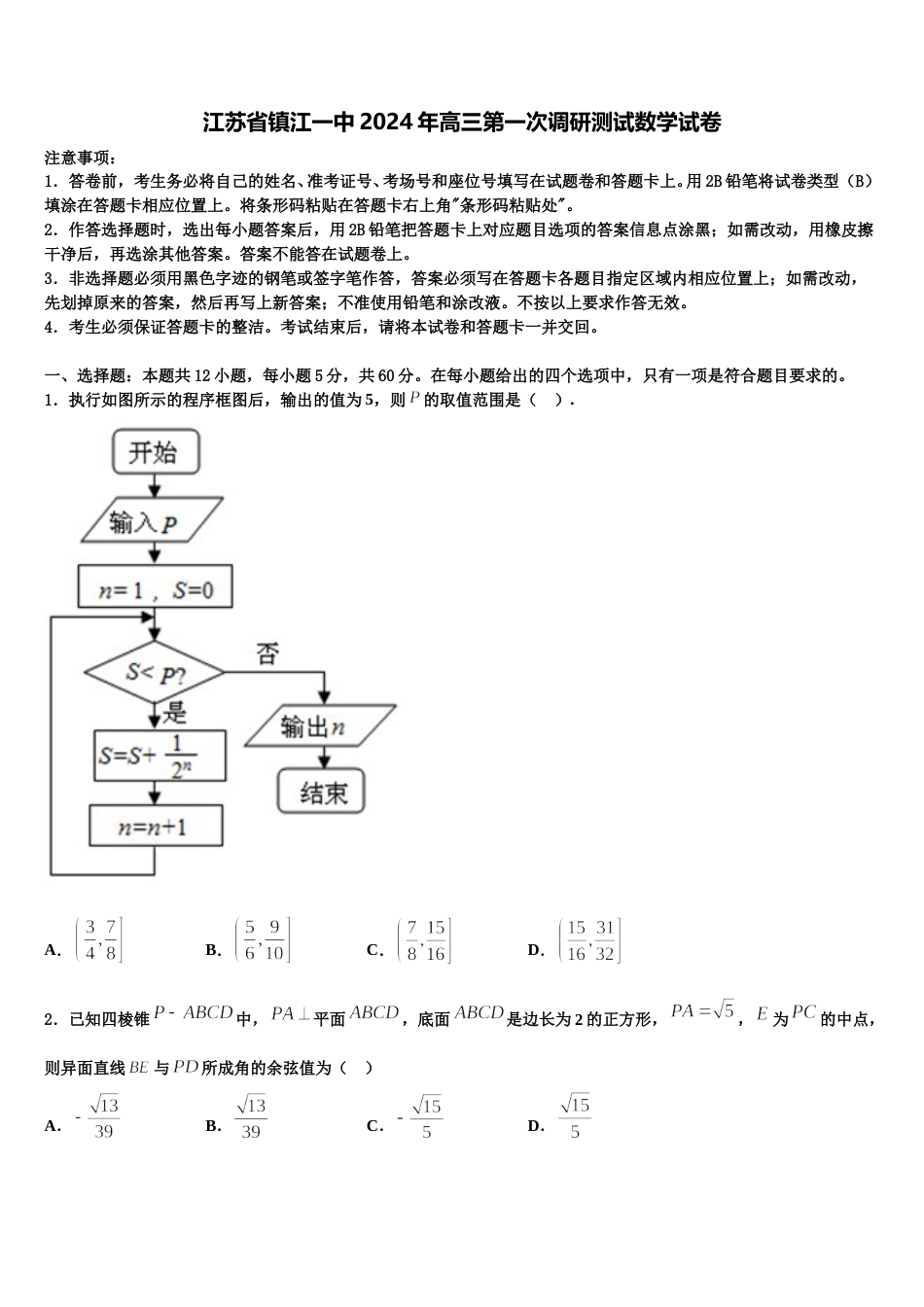
江苏省镇江一中 2024 年高三第一次调研测试数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用 2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.执行如图所示的程序框图后,输出的值为 5,则的取值范围是( ). A.B.C.D.2.已知四棱锥中,平面,底面是边长为 2 的正方形,,为的中点,则异面直线与所成角的余弦值为( )A.B.C.D.3.已知集合,,,则( )A.B.C.D.4.小张家订了一份报纸,送报人可能在早上之间把报送到小张家,小张离开家去工作的时间在早上之间.用表示事件:“小张在离开家前能得到报纸”,设送报人到达的时间为,小张离开家的时间为,看成平面中的点,则用几何概型的公式得到事件的概率等于( )A.B.C.D.5.在中,已知,,,为线段上的一点,且,则的最小值为( )A.B.C.D.6.函数的定义域为( )A.B.C.D.7.已知是定义在上的奇函数,且当时,.若,则的解集是( )A.B.C.D.8.函数()的图像可以是( )A.B.C.D.9.已知函数的图像与一条平行于轴的直线有两个交点,其横坐标分别为,则( )A.B.C.D.10.如图所示是某年第一季度五省 GDP 情况图,则下列说法中不正确的是( )A.该年第一季度 GDP 增速由高到低排位第 3 的是山东省B.与去年同期相比,该年第一季度的 GDP 总量实现了增长C.该年第一季度 GDP 总量和增速由高到低排位均居同一位的省份有 2 个D.去年同期浙江省的 GDP 总量超过了 4500 亿元11.已知函数若关于的方程有六个不相等的实数根,则实数的取值范围为( )A.B.C.D.12.已知在平面直角坐标系中,圆:与圆:交于,两点,若,则实数的值为( )A.1B.2C.-1D.-2二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.在△ABC 中,∠BAC=,AD 为∠BAC 的角平分线,且,若 AB=2,则 BC=_______.14.已知各棱长都相等的直三棱柱(侧棱与底面垂直的棱柱称为直棱柱)所有顶点都在球的表面上.若球的表面积为则该三棱柱的侧面积为___________.15.在中,点在边上,且,设,,则________(用,表示)16.在三棱锥中,,,两两垂直且,点为的外接球上任意一点,则的最大值为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知是递增的等比数列,,且、、成等差数列.(Ⅰ)求数列的通项公式;(Ⅱ)设,,求数列的前项和.18.(12 分)已知等差数列和等比数列的各项均为整数,它们的前项和分别为,且,.(1)求数列,的通项公式;(2)求;(3)是否存在正整数,使得恰好是数列或中的项?若存在,求出所有满足条件的的值;若不存在,说明理由.19.(12 分)在平面直角坐标系中,点,直线 的参数方程为为参数),以坐标原点为极点,以轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)求曲线的直角坐标方程;(2)若直线 与曲线相交于不同的两点是线段的中点,当时,求的值.20.(12 分)已知函数.(1)讨论的单调性;(2)若恒成立,求实数的取值范围.21.(12 分)定义:若数列满足所有的项均由构成且其中有个, 有个,则称为“﹣数列”.(1)为“﹣数列”中的任意三项,则使得的取法有多少种?(2)为“﹣数列”中的任意三项,则存在多少正整数对使得且的概率为.22.(10 分)在直角坐标系 xOy 中,直线 的参数方程为(t 为参数)....