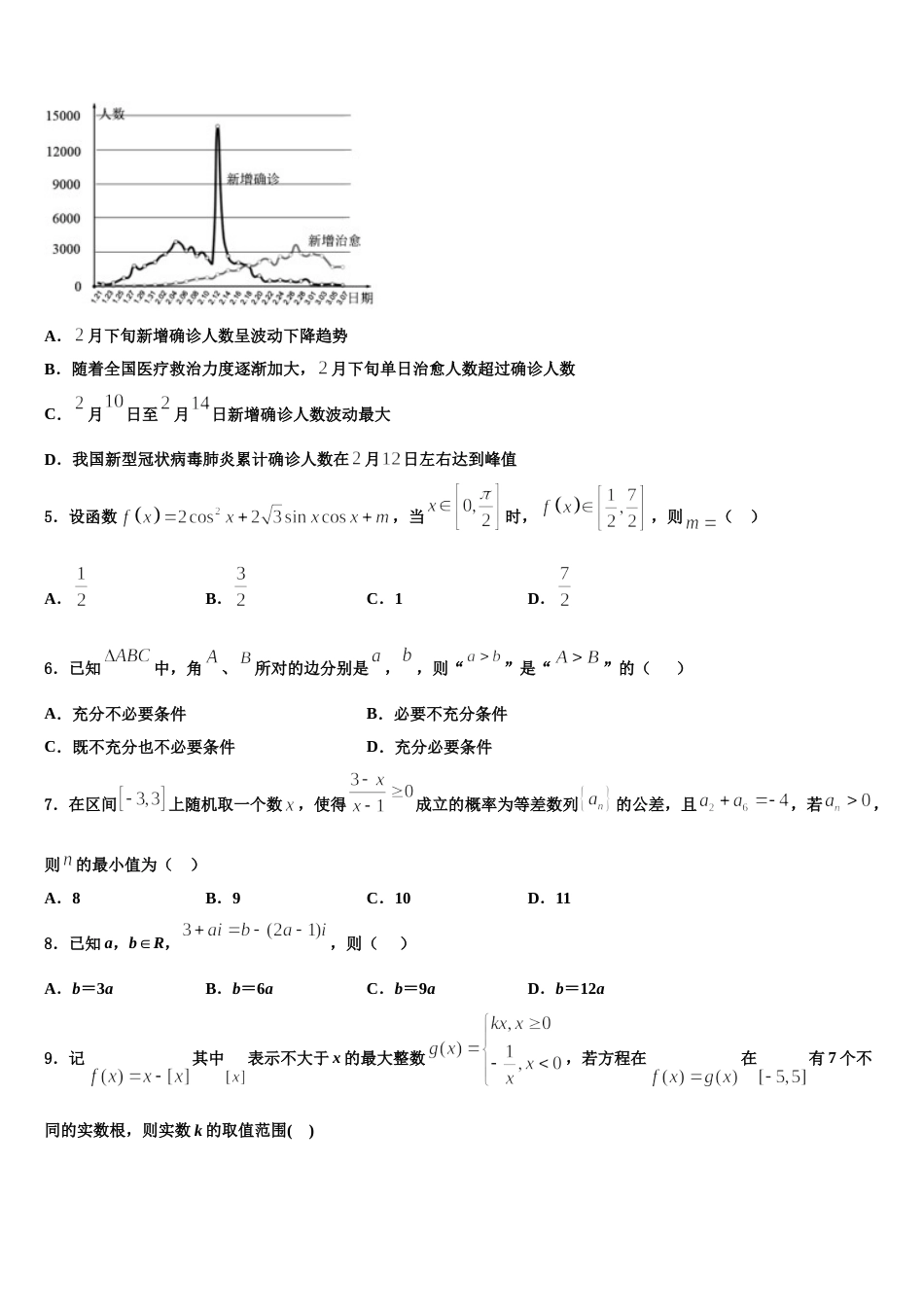
江苏省镇江市丹徒高级中学 2024 届高考仿真卷数学试题注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若复数满足,则( )A.B.C.D.2.函数,,的部分图象如图所示,则函数表达式为( )A.B.C.D.3.在中,角的对边分别为,,若,,且,则的面积为( )A.B.C.D.4.年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒蔓延,各级政府相继启动重大突发公共卫生事件一级响应,全国人心抗击疫情.下图表示 月日至月日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,则下列中表述错误的是( )A.月下旬新增确诊人数呈波动下降趋势B.随着全国医疗救治力度逐渐加大,月下旬单日治愈人数超过确诊人数C.月日至月日新增确诊人数波动最大D.我国新型冠状病毒肺炎累计确诊人数在月日左右达到峰值5.设函数,当时,,则( )A.B.C.1D.6.已知中,角、所对的边分别是,,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充分必要条件7.在区间上随机取一个数,使得成立的概率为等差数列的公差,且,若,则的最小值为( )A.8B.9C.10D.118.已知 a,b∈R,,则( )A.b=3aB.b=6aC.b=9aD.b=12a9.记其中表示不大于 x 的最大整数,若方程在在有 7 个不同的实数根,则实数 k 的取值范围( )A.B.C.D.10.已知定义在上的奇函数和偶函数满足(且),若,则函数的单调递增区间为( )A.B.C.D.11.若函数函数只有 1 个零点,则的取值范围是( )A.B.C.D.12.定义在上函数满足,且对任意的不相等的实数有成立,若关于 x 的不等式在上恒成立,则实数 m 的取值范围是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知角的终边过点,则______.14.已知函数,若关于的方程恰有四个不同的解,则实数的取值范围是______.15.某校高二(4)班统计全班同学中午在食堂用餐时间,有 7 人用时为 6 分钟,有 14 人用时 7 分钟,有 15 人用时为8 分钟,还有 4 人用时为 10 分钟,则高二(4)班全体同学用餐平均用时为____分钟.16.已知抛物线,点为抛物线上一动点,过点作圆的切线,切点分别为,则线段长度的取值范围为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图,在四棱锥中,四边形为正方形,平面,点是棱的中点,,.(1)若,证明:平面平面;(2)若三棱锥的体积为,求二面角的余弦值.18.(12 分)已知椭圆的右焦点为,过点且斜率为的直线 与椭圆交于两点,线段的中点为为坐标原点.(1)证明:点在轴的右侧;(2)设线段的垂直平分线与轴、轴分别相交于点.若与的面积相等,求直线 的斜率19.(12 分)如图,四棱锥中,底面是边长为的菱形,,点分别是的中点.(1)求证:平面;(2)若,求直线与平面所成角的正弦值.20.(12 分)已知.(1)若曲线在点处的切线也与曲线相切,求实数的值;(2)试讨论函数零点的个数.21.(12 分)为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北、湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区,在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:普查对象类别顺利不顺利合计企事业单位401050个体经营户10050150合计14060200(1)写出选择 5 个国家综合试点地区采用的抽样方法;(2)根据列联表判断是否有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别...