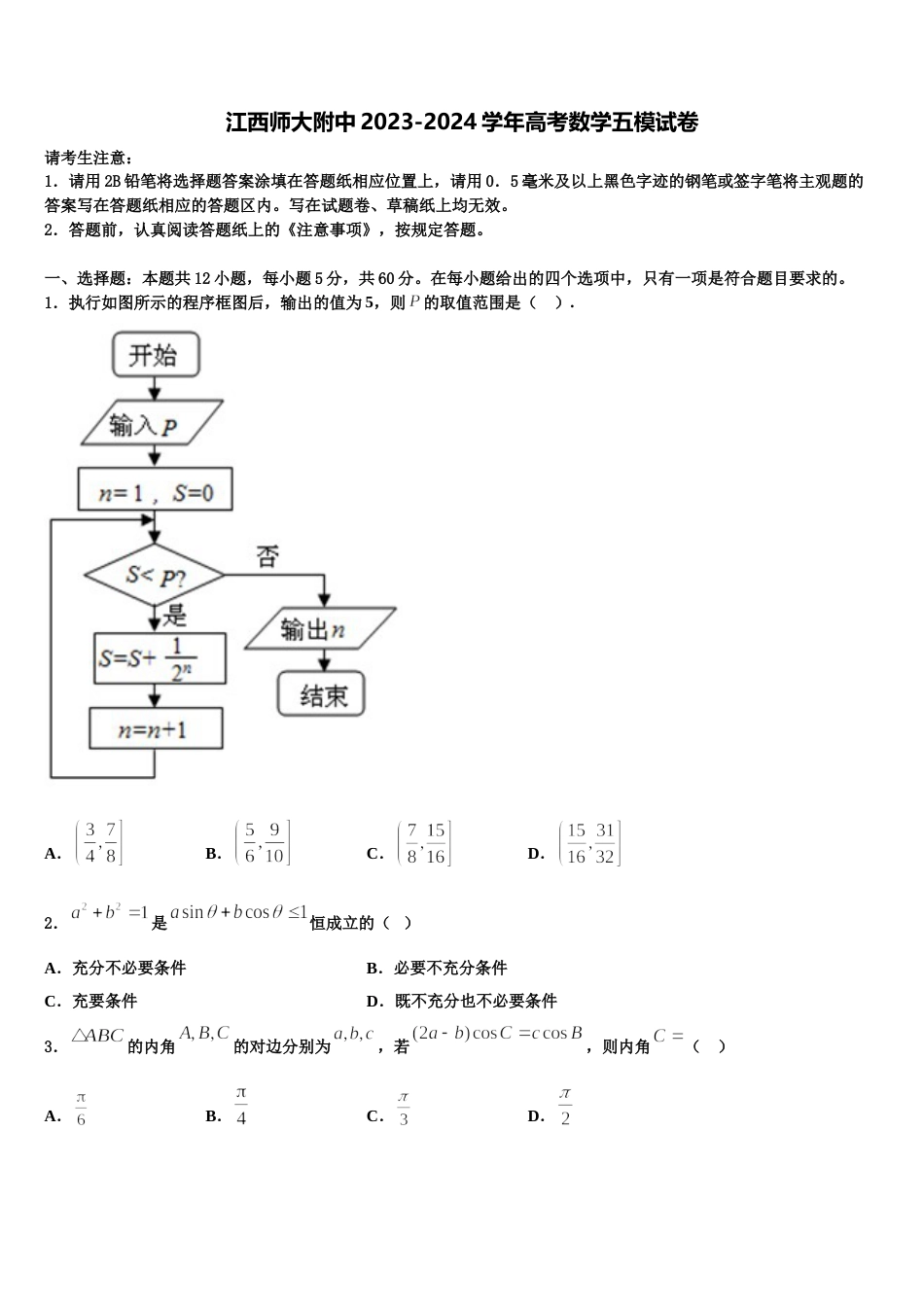
江西师大附中 2023-2024 学年高考数学五模试卷请考生注意:1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5 毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.执行如图所示的程序框图后,输出的值为 5,则的取值范围是( ). A.B.C.D.2.是恒成立的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.的内角的对边分别为,若,则内角( )A.B.C.D.4.已知( 为虚数单位,为的共轭复数),则复数在复平面内对应的点在( ).A.第一象限B.第二象限C.第三象限D.第四象限5.定义域为 R 的偶函数满足任意,有,且当时,.若函数至少有三个零点,则的取值范围是( )A.B.C.D.6.已知函数()的最小值为 0,则( )A.B.C.D.7.已知、分别是双曲线的左、右焦点,过作双曲线的一条渐近线的垂线,分别交两条渐近线于点、,过点作轴的垂线,垂足恰为,则双曲线的离心率为( )A.B.C.D.8.若函数,在区间上任取三个实数,,均存在以,,为边长的三角形,则实数的取值范围是( )A.B.C.D.9.已知 a,b 是两条不同的直线,α,β 是两个不同的平面,且,,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10.已知函数,,若,对任意恒有,在区间上有且只有一个使,则的最大值为( )A.B.C.D.11.已知定义在上的函数满足,且当时,.设在上的最大值为(),且数列的前项的和为.若对于任意正整数不等式恒成立,则实数的取值范围为( )A.B.C.D.12.将函数向左平移个单位,得到的图象,则满足( )A.图象关于点对称,在区间上为增函数B.函数最大值为 2,图象关于点对称C.图象关于直线对称,在上的最小值为 1D.最小正周期为,在有两个根二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知向量,,若,则______.14.已知函数为奇函数,,且与图象的交点为,,…,,则______.15.函数的定义域是____________.(写成区间的形式)16.命题“对任意,”的否定是 .三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知函数 f(x)ax﹣lnx(a∈R).(1)若 a=2 时,求函数 f(x)的单调区间;(2)设 g(x)=f(x)1,若函数 g(x)在上有两个零点,求实数 a 的取值范围.18.(12 分)已知某种细菌的适宜生长温度为 12℃~27℃,为了研究该种细菌的繁殖数量(单位:个)随温度(单位:℃)变化的规律,收集数据如下:温度/℃14161820222426繁殖数量/个2530385066120218对数据进行初步处理后,得到了一些统计量的值,如表所示:20784.11123.8159020.5其中,.(1)请绘出关于的散点图,并根据散点图判断与哪一个更适合作为该种细菌的繁殖数量关于温度的回归方程类型(给出判断即可,不必说明理由);(2)根据(1)的判断结果及表格数据,建立关于的回归方程(结果精确到 0.1);(3)当温度为 27℃时,该种细菌的繁殖数量的预报值为多少?参考公式:对于一组数据,其回归直线的斜率和截距的最小二成估计分别为,,参考数据:.19.(12 分)已知椭圆的离心率为,且过点.(1)求椭圆 C 的标准方程;(2)点 P 是椭圆上异于短轴端点 A,B 的任意一点,过点 P 作轴于 Q,线段 PQ 的中点为 M.直线 AM 与直线交于点 N,D 为线段 BN 的中点,设 O 为坐标原点,试判断以 OD 为直径的圆与点 M 的位置关系.20.(12 分)在四棱锥中,底面为直角梯形,,,,,,,分别为,的中点.(1)求证:.(2)若,求二面角的余弦值.21.(12 分)已知函数.(1)若函数,求的极值;(2)证明:. (参考数据: )22.(10 分)设函数.(1)时,求的单调区间;(2)当时,设的最小值为,若恒成立,求实数 t 的取值范围.参考答案...