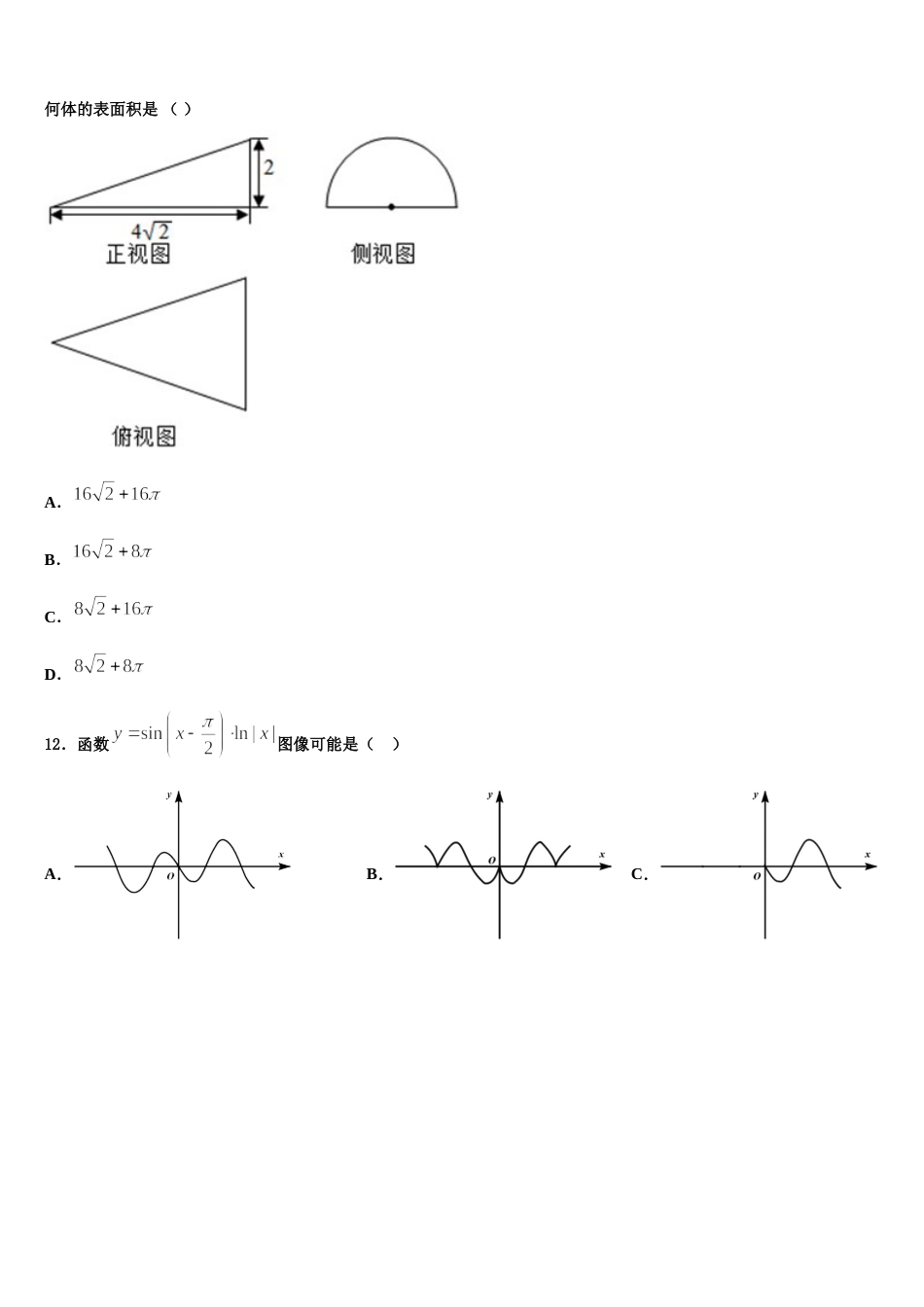
江西省宁都县宁师中学 2023-2024 学年高考冲刺数学模拟试题注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。2.答题时请按要求用笔。3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若的展开式中的系数为 150,则( )A.20B.15C.10D.252.设直线 过点,且与圆:相切于点,那么( )A.B.3C.D.13.复数的共轭复数记作,已知复数对应复平面上的点,复数:满足.则等于( )A.B.C.D.4.已知全集,则集合的子集个数为( )A.B.C.D.5.2019 年末,武汉出现新型冠状病毒肺炎()疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从 2 月 7 日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户 6 口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为()且相互独立,该家庭至少检测了 5 个人才能确定为“感染高危户”的概率为,当时,最大,则( )A.B.C.D.6.设,是双曲线的左,右焦点,是坐标原点,过点作的一条渐近线的垂线,垂足为.若,则的离心率为( )A.B.C.D.7.某四棱锥的三视图如图所示,则该四棱锥的表面积为( )A.8B.C.D.8.已知等差数列满足,公差,且成等比数列,则A.1B.2C.3D.49.单位正方体 ABCD-,黑、白两蚂蚁从点 A 出发沿棱向前爬行,每走完一条棱称为“走完一段”.白蚂蚁爬地的路线是 AA1→A1D1→‥,黑蚂蚁爬行的路线是 AB→BB1→‥,它们都遵循如下规则:所爬行的第 i+2 段与第 i段所在直线必须是异面直线(iN*).设白、黑蚂蚁都走完 2020 段后各自停止在正方体的某个顶点处,这时黑、白两蚂蚁的距离是( )A.1B.C.D.010.已知随机变量服从正态分布,,( )A.B.C.D.11.一个几何体的三视图及尺寸如下图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是 ( ) A.B.C.D.12.函数图像可能是( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知,满足约束条件,则的最小值为__________.14.如图,在棱长为 2 的正方体中,点、分别是棱,的中点,是侧面正方形内一点(含边界),若平面,则线段长度的取值范围是______.15.执行如图所示的程序框图,则输出的结果是______.16.已知四棱锥,底面四边形为正方形,,四棱锥的体积为,在该四棱锥内放置一球,则球体积的最大值为_________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知抛物线:,点为抛物线的焦点,焦点到直线的距离为,焦点到抛物线的准线的距离为,且.(1)求抛物线的标准方程;(2)若轴上存在点,过点的直线 与抛物线相交于、两点,且为定值,求点的坐标.18.(12 分)若养殖场每个月生猪的死亡率不超过,则该养殖场考核为合格,该养殖场在 2019 年 1 月到 8 月养殖生猪的相关数据如下表所示:月份1 月2 月3 月4 月5 月6 月7 月8 月月养殖量/千只 33456791012月利润/十万元3.64.14.45.26.27.57.99.1生猪死亡数/只293749537798126145(1)从该养殖场 2019 年 2 月到 6 月这 5 个月中任意选取 3 个月,求恰好有 2 个月考核获得合格的概率;(2)根据 1 月...