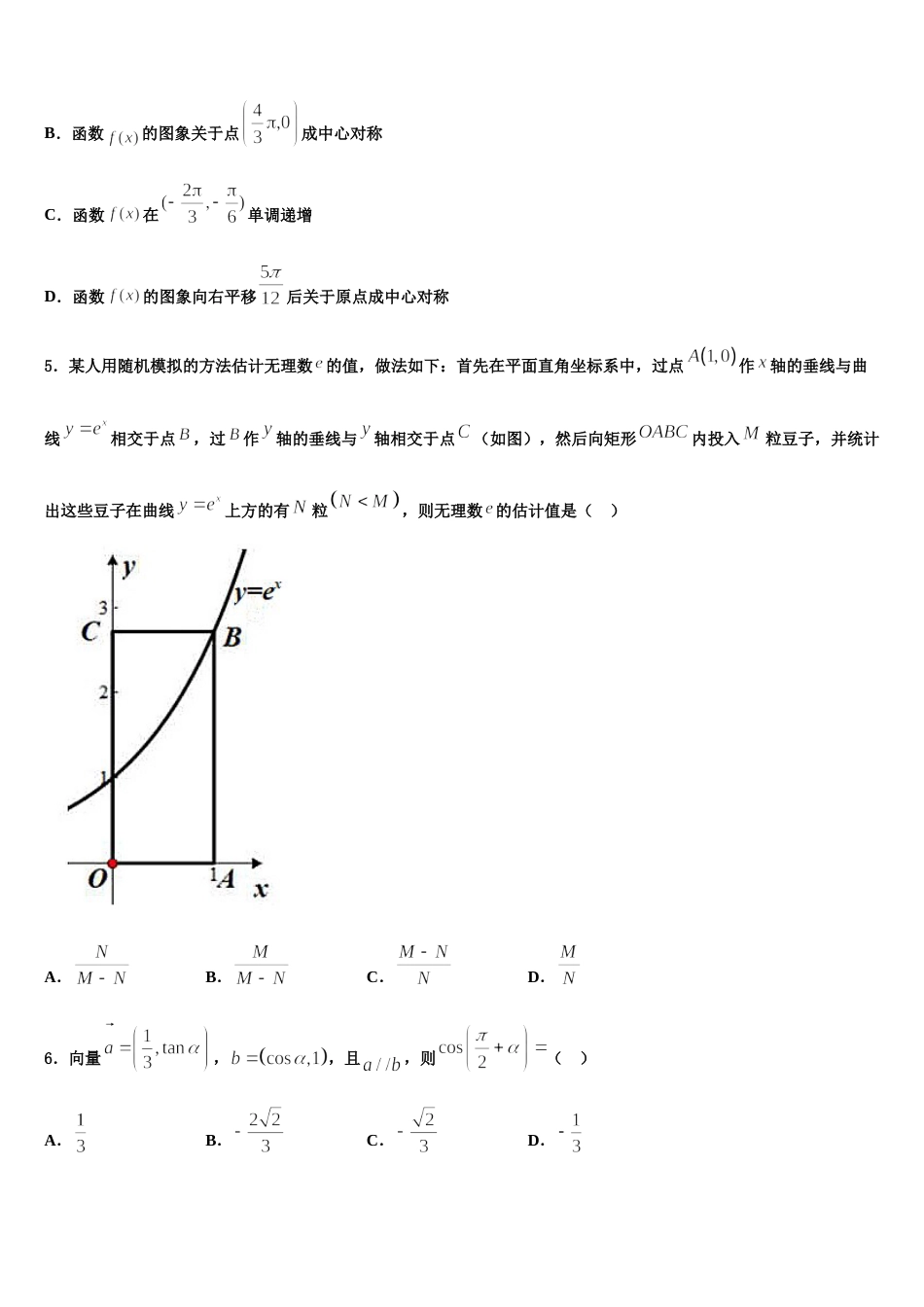
江西省宜春市宜丰中学 2024 年高考全国统考预测密卷数学试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。3.考试结束后,将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知命题:R,;命题 :R,,则下列命题中为真命题的是( )A.B.C.D.2.盒中装有形状、大小完全相同的 5 张“刮刮卡”,其中只有 2 张“刮刮卡”有奖,现甲从盒中随机取出 2 张,则至少有一张有奖的概率为( )A.B.C.D.3.已知抛物线的焦点与双曲线的一个焦点重合,且抛物线的准线被双曲线截得的线段长为,那么该双曲线的离心率为( )A.B.C.D.4.函数的部分图象如图中实线所示,图中圆与的图象交于两点,且在轴上,则下列说法中正确的是A.函数的最小正周期是B.函数的图象关于点成中心对称C.函数在单调递增D.函数的图象向右平移后关于原点成中心对称5.某人用随机模拟的方法估计无理数 的值,做法如下:首先在平面直角坐标系中,过点作轴的垂线与曲线相交于点,过作轴的垂线与轴相交于点(如图),然后向矩形内投入粒豆子,并统计出这些豆子在曲线上方的有粒,则无理数 的估计值是( ) A.B.C.D.6.向量,,且,则( )A.B.C.D.7.已知双曲线:,,为其左、右焦点,直线 过右焦点,与双曲线的右支交于,两点,且点在轴上方,若,则直线 的斜率为( )A.B.C.D.8.某医院拟派 2 名内科医生、3 名外科医生和 3 名护士共 8 人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有A.72 种B.36 种C.24 种D.18 种9.已知双曲线的右焦点为,过的直线 交双曲线的渐近线于两点,且直线 的倾斜角是渐近线倾斜角的 2 倍,若,则该双曲线的离心率为( )A.B.C.D.10.复数的共轭复数记作,已知复数对应复平面上的点,复数:满足.则等于( )A.B.C.D.11.函数在上单调递减的充要条件是( )A.B.C.D.12.已知平面向量,满足,,且,则( )A.3B.C.D.5二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知椭圆 C:1(a>b>0)的左、右焦点分别为 F1,F2,椭圆的焦距为 2c,过 C 外一点 P(c,2c)作线段PF1,PF2分别交椭圆 C 于点 A、B,若|PA|=|AF1|,则_____.14.已知椭圆 Г:,F1、F2是椭圆 Г 的左、右焦点,A 为椭圆 Г 的上顶点,延长 AF2交椭圆 Г 于点 B,若为等腰三角形,则椭圆 Г 的离心率为___________.15.已知无盖的圆柱形桶的容积是立方米,用来做桶底和侧面的材料每平方米的价格分别为 30 元和 20 元,那么圆桶造价最低为________元.16.下图是一个算法流程图,则输出的的值为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)若关于的方程的两根都大于 2,求实数的取值范围.18.(12 分)在平面直角坐标系中,曲线 C 的参数方程为(为参数).以原点为极点,x 轴的非负半轴为极轴,建立极坐标系.(1)求曲线 C 的极坐标方程;(2)直线(t 为参数)与曲线 C 交于 A,B 两点,求最大时,直线 l 的直角坐标方程.19.(12 分)已知函数(I)若讨论的单调性;(Ⅱ)若,且对于函数的图象上两点,存在,使得函数的图象在处的切线.求证:.20.(12 分)已知函数,.(1)若,,求实数 的值.(2)若,,求正实数的取值范围.21.(12 分)已知首项为 2 的数列满足.(1)证明:数列是等差数列.(2)令,求数列的前项和.22.(10 分)如图,在四棱锥 P—ABCD 中,四边形 ABCD 为平行四边形,BD⊥DC,△PCD 为正三角形,平面PCD⊥平面 ABCD,E 为 PC 的中点. (1)证明:AP∥平面 EBD;(2)证明:BE⊥PC.参考答案一、选择...