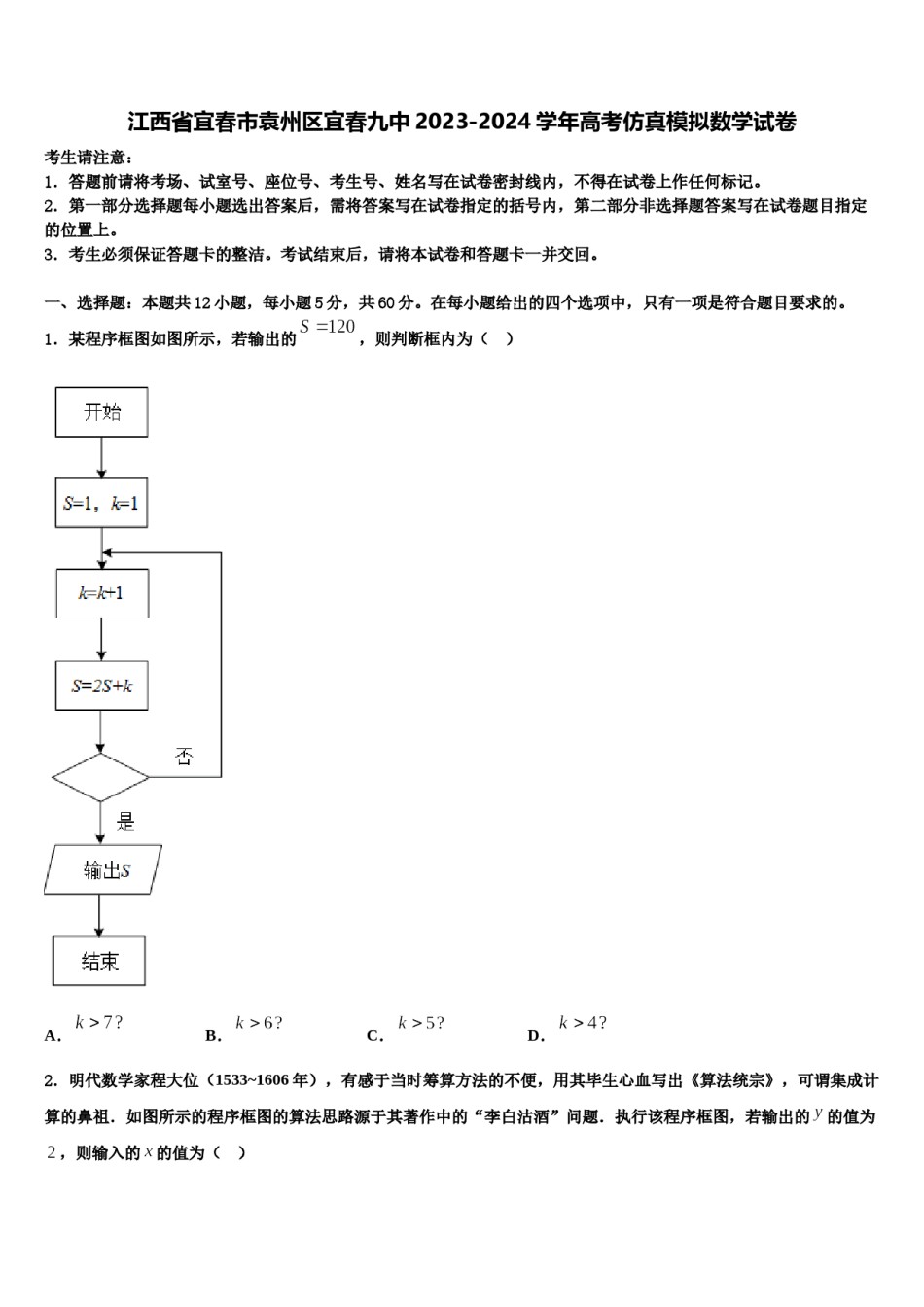
江西省宜春市袁州区宜春九中2023-2024学年高考仿真模拟数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某程序框图如图所示,若输出的,则判断框内为()A.B.C.D.2.明代数学家程大位(1533~1606年),有感于当时筹算方法的不便,用其毕生心血写出《算法统宗》,可谓集成计算的鼻祖.如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题.执行该程序框图,若输出的的值为,则输入的的值为()A.B.C.D.3.命题:存在实数,对任意实数,使得恒成立;:,为奇函数,则下列命题是真命题的是()A.B.C.D.4.已知函数,要得到函数的图象,只需将的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度5.二项式展开式中,项的系数为()A.B.C.D.上任意一点,,若线段的垂直平分线交直线于点,则点6.已知为圆:的轨迹方程为()B.A.C.()D.()7.已知a,b是两条不同的直线,α,β是两个不同的平面,且,,则“”是“”的()B.必要不充分条件C.充要条件D.既不充分也不必要条件A.充分不必要条件8.复数的模为().A.B.1C.2D.9.如图,中,点D在BC上,,将沿AD旋转得到三棱锥,分别记,与平面ADC所成角为,,则,的大小关系是()A.B.C.,两种情况都存在D.存在某一位置使得10.在中,,,,若,则实数()A.B.C.D.11.已知向量,则()A.∥B.⊥C.∥()D.⊥()12.如图1,《九章算术》中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是:有一根竹子,原高一丈(1丈=10尺),现被风折断,尖端落在地上,竹尖与竹根的距离三尺,问折断处离地面的高为()尺.A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.已知函数,若关于的方程在定义域上有四个不同的解,则实数的取值范围是_______.14.将2个相同的红球和2个相同的黑球全部放入甲、乙、丙、丁四个盒子里,其中甲、乙盒子均最多可放入2个球,丙、丁盒子均最多可放入1个球,且不同颜色的球不能放入同一个盒子里,共有________种不同的放法.15.已知△的三个内角为,,,且,,成等差数列,则的最小值为,(1)求数列的首__________,最大值为___________.16.已知,则__________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。,已知17.(12分)设数列是等比数列,项和公比;(2)求数列的通项公式.18.(12分)已知抛物线,焦点为,直线交抛物线于两点,交抛物线的准线于点,如图所示,当直线经过焦点时,点恰好是的中点,且.(1)求抛物线的方程;的斜率分别是,当直线的纵截距为1时,有数列满足(2)点是原点,设直线,设数列的前n项和为,已知存在正整数使得,求m的值.中,曲线上的任意一点到直线的距离比点到点的距离小1.19.(12分)在直角坐标系(1)求动点的轨迹的方程;(2)若点是圆上一动点,过点作曲线的两条切线,切点分别为,求直线斜率的取值范围.20.(12分)已知数列是各项均为正数的等比数列,数列为等差数列,且,,.(1)求数列与的通项公式;(2)求数列的前项和;(3)设为数列的前项和,若对于任意,有,求实数的值.21.(12分)已知函数(1)若,求证:(2)若,恒有,求实数的取值范围.上任意一点,直线22.(10分)已知点为椭圆与圆交于,两点,点为椭圆的左焦点.(1)求证:直线与椭圆相切;(2)判断是否为定值,并说明理由.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】程序在运行过程中各变量值变化如下表:KS是否继续循环循环前11第一圈24是第二圈311是第三圈426是第四圈557是第五圈6120否故退出循环的...