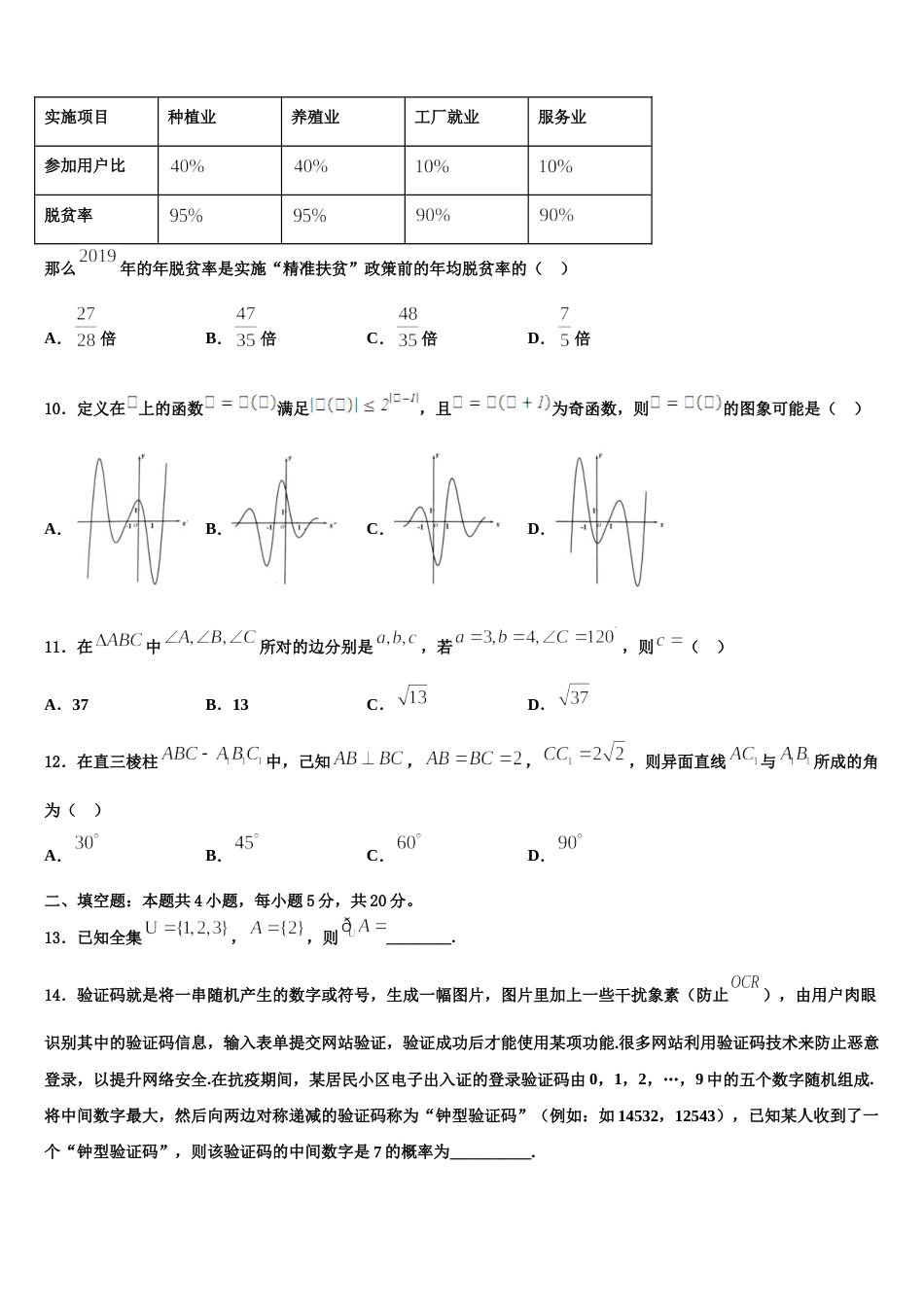
河北省中原名校 2024 届高三下学期第六次检测数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数,若对于任意的,函数在内都有两个不同的零点,则实数的取值范围为( )A.B.C.D.2.一辆邮车从地往地运送邮件,沿途共有地,依次记为,,…(为地,为地).从地出发时,装上发往后面地的邮件各 1 件,到达后面各地后卸下前面各地发往该地的邮件,同时装上该地发往后面各地的邮件各 1 件,记该邮车到达,,…各地装卸完毕后剩余的邮件数记为.则的表达式为( ).A.B.C.D.3.已知集合,则全集则下列结论正确的是( )A.B.C.D.4.某几何体的三视图如图所示(单位:),则该几何体的体积(单位:)为( )A.B.6C.D.5.双曲线的离心率为,则其渐近线方程为A.B.C.D.6.设双曲线的右顶点为,右焦点为,过点作平行的一条渐近线的直线与交于点,则的面积为( )A.B.C.5D.67.已知定义在上的偶函数,当时,,设,则( )A.B.C.D.8.已知函数的图象如图所示,则可以为( )A.B.C.D.9.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在 2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为.2015 年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中 2019 年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:实施项目种植业养殖业工厂就业服务业参加用户比脱贫率那么年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( )A.倍B.倍C.倍D.倍10.定义在 上的函数满足,且为奇函数,则的图象可能是( )A.B.C.D.11.在中所对的边分别是,若,则( )A.37B.13C.D.12.在直三棱柱中,己知,,,则异面直线与所成的角为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知全集,,则________.14.验证码就是将一串随机产生的数字或符号,生成一幅图片,图片里加上一些干扰象素(防止),由用户肉眼识别其中的验证码信息,输入表单提交网站验证,验证成功后才能使用某项功能.很多网站利用验证码技术来防止恶意登录,以提升网络安全.在抗疫期间,某居民小区电子出入证的登录验证码由 0,1,2,…,9 中的五个数字随机组成.将中间数字最大,然后向两边对称递减的验证码称为“钟型验证码”(例如:如 14532,12543),已知某人收到了一个“钟型验证码”,则该验证码的中间数字是 7 的概率为__________.15.函数在处的切线方程是____________.16.已知关于空间两条不同直线 m、n,两个不同平面、,有下列四个命题:①若且,则;②若且,则;③若且,则;④若,且,则.其中正确命题的序号为______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)设,,其中.(1)当时,求的值;(2)对,证明:恒为定值.18.(12 分)已知数列的前 n 项和,是等差数列,且.(Ⅰ)求数列的通项公式;(Ⅱ)令.求数列的前 n 项和.19.(12 分)设函数 f(x)=x2−4xsinx−4cosx. (1)讨论函数 f(x)在[−π,π]上的单调性;(2)证明:函数 f(x)在 R 上有且仅有两个零点.20.(12 分)在中,内角 A,B,C 的对边分别为 a,b,c,且满足.(1)求 B;(2)若,AD 为 BC 边上的中线,当的面积取得最大值时,求 AD 的长.21.(12 分)已知函数.(1)当时,求函数的图象在处的切线方程;(2)讨论函数的单调性;(3)当时,若方程有两个不相等的实数根,求证:.22.(10 分)某工厂生产某种电子产品,每件产品不合格的概率均为,现工厂为提高产品...