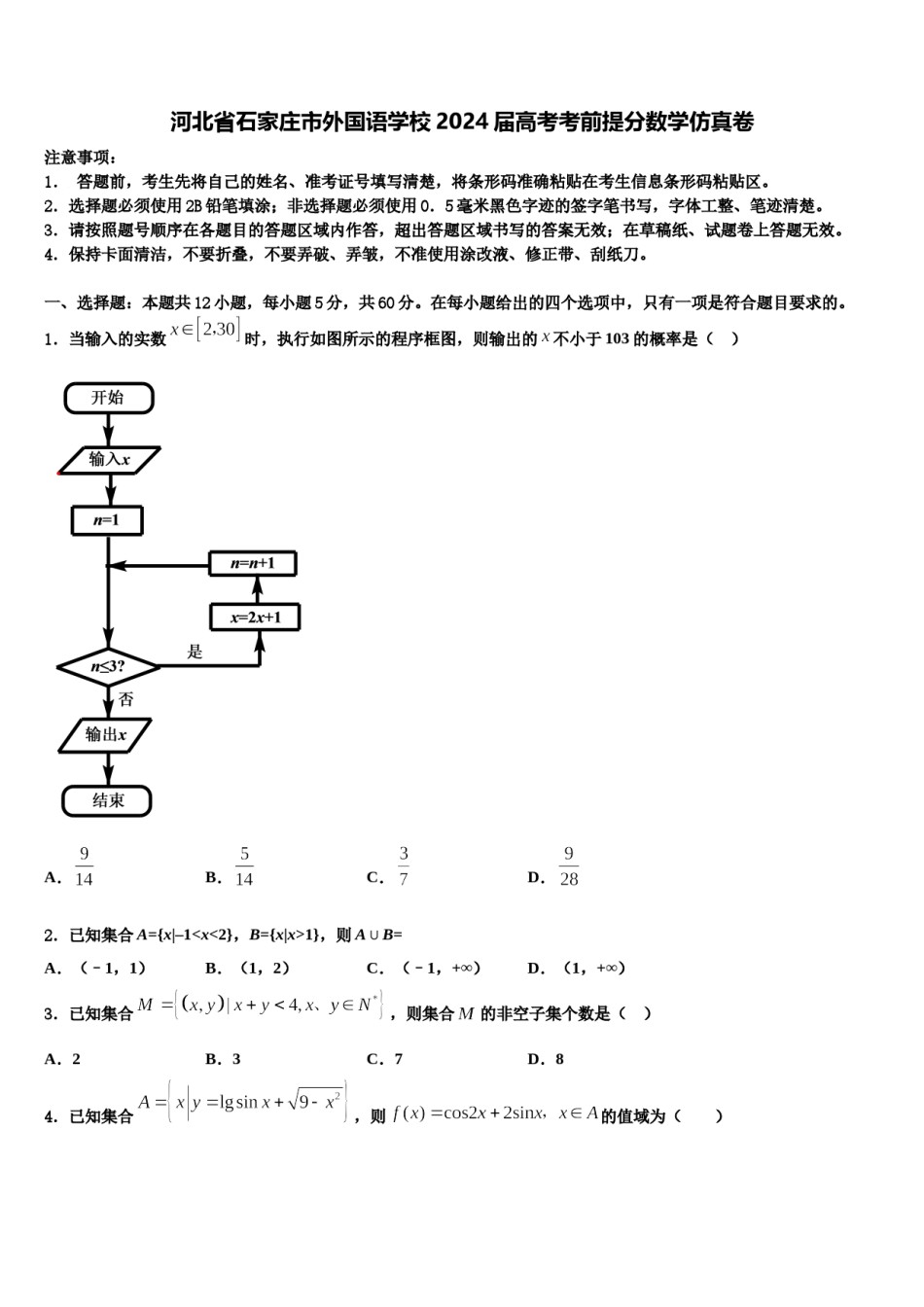
河北省石家庄市外国语学校2024届高考考前提分数学仿真卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.当输入的实数时,执行如图所示的程序框图,则输出的不小于103的概率是()A.B.C.D.2.已知集合A={x–1<x<2},B={xx>1},则A∪B=A.(–1,1)B.(1,2)C.(–1,+∞)D.(1,+∞)3.已知集合,则集合的非空子集个数是()A.2B.3C.7D.84.已知集合,则的值域为()A.B.C.D.5.“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件6.已知三点A(1,0),B(0,),C(2,),则△ABC外接圆的圆心到原点的距离为()A.B.C.D.7.已知函数在上单调递增,则的取值范围()A.B.C.D.8.在中,角所对的边分别为,已知,.当变化时,若存在最大值,D.则正数的取值范围为A.B.C.9.在声学中,声强级(单位:)由公式给出,其中为声强(单位:).,,那么()A.B.C.D.10.已知函数,若关于的方程恰好有3个不相等的实数根,则实数的取值范D.围为()分别是椭圆的左、右焦点,若点为上的任意一A.B.C.11.已知椭圆的短轴长为2,焦距为点,则的取值范围为()A.B.C.D.12.设直线的方程为,圆的方程为,若直线被圆所截得的弦长为,则实数的取值为A.或11B.或11C.D.二、填空题:本题共4小题,每小题5分,共20分。13.设,若关于的方程有实数解,则实数的取值范围_____.14.过动点作圆:的切线,其中为切点,若(为坐标原点),则的最小值是__________.15.已知实数,满足则的取值范围是______.16.三所学校举行高三联考,三所学校参加联考的人数分别为160,240,400,为调查联考数学学科的成绩,现采用分层抽样的方法在这三所学校中抽取样本,若在学校抽取的数学成绩的份数为30,则抽取的样本容量为____________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知满足,且,求的值及的面积.(从①,②,③这三个条件中选一个,补充到上面问题中,并完成解答.)18.(12分)如图所示,在三棱锥中,,,,点为中点.(1)求证:平面平面;(2)若点为中点,求平面与平面所成锐二面角的余弦值.19.(12分)已知数列满足:对一切成立.(1)求数列的通项公式;(2)求数列的前项和.20.(12分)在直角坐标系x0y中,把曲线α为参数)上每个点的横坐标变为原来的倍,纵坐标不变,得到曲线以坐标原点为极点,以x轴正半轴为极轴,建立极坐标系,曲线的极坐标方程(1)写出的普通方程和的直角坐标方程;(2)设点M在上,点N在上,求MN的最小值以及此时M的直角坐标.21.(12分)设函数.(1)当时,解不等式;(2)设,且当时,不等式有解,求实数的取值范围.22.(10分)在①,②,③这三个条件中任选一个,补充在下面问题中,求的面积的值(或最大值).已知的内角,,所对的边分别为,,,三边,,与面积满足关系式:,且,求的面积的值(或最大值).参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】根据循环结构的运行,直至不满足条件退出循环体,求出的范围,利用几何概型概率公式,即可求出结论.【详解】程序框图共运行3次,输出的的范围是,所以输出的不小于103的概率为.故选:A.【点睛】本题考查循环结构输出结果、几何概型的概率,模拟程序运行是解题的关键,属于基础题.2、C【解析】根据并集的求法直接求出结果.【详解】 ,∴,故选C.【点睛】考查并集的求法,属于基础题.3、C【解析】先确定集合中元素,可得非空子集个数.【详解】由题意,共3个元素,其...