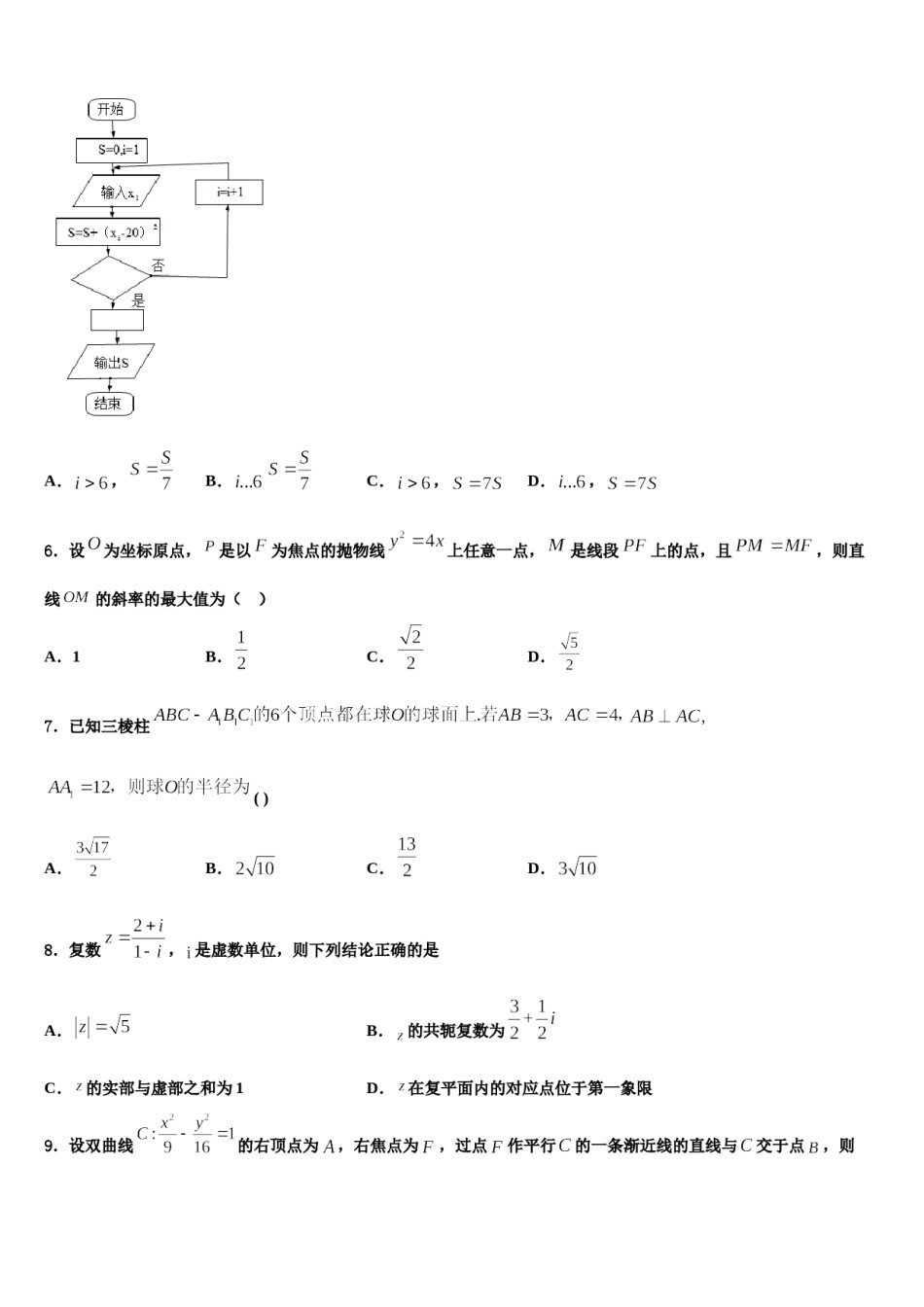
河南省安阳市林州一中2023-2024学年高考数学必刷试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在各项均为正数的等比数列中,若,则()A.B.6C.4D.52.设全集,集合,则=()A.B.C.D.3.在条件下,目标函数的最大值为40,则的最小值是()A.B.C.D.24.若复数,,其中是虚数单位,则的最大值为()A.B.C.D.5.框图与程序是解决数学问题的重要手段,实际生活中的一些问题在抽象为数学模型之后,可以制作框图,编写程序,得到解决,例如,为了计算一组数据的方差,设计了如图所示的程序框图,其中输入,,,,,,,则图中空白框中应填入()A.,B.C.,D.,6.设为坐标原点,是以为焦点的抛物线上任意一点,是线段上的点,且,则直线的斜率的最大值为()D.A.1B.C.7.已知三棱柱()A.B.C.D.8.复数,是虚数单位,则下列结论正确的是A.B.的共轭复数为C.的实部与虚部之和为1D.在复平面内的对应点位于第一象限9.设双曲线的右顶点为,右焦点为,过点作平行的一条渐近线的直线与交于点,则的面积为()A.B.C.5D.610.在直三棱柱中,己知,,,则异面直线与所成的角为()A.B.C.D.11.已知直线,,则“”是“”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件12.已知复数,则()A.B.C.D..已知过原点且相互垂直的两条直线和,其中二、填空题:本题共4小题,每小题5分,共20分。13.在平面直角坐标系中,圆与圆相交于,两点,与圆相切于点.若,则直线的斜率为_____________.14.已知数列的前项和为,且满足,则______15.设为椭圆在第一象限上的点,则的最小值为________.16.在一次医疗救助活动中,需要从A医院某科室的6名男医生、4名女医生中分别抽调3名男医生、2名女医生,且男医生中唯一的主任医师必须参加,则不同的选派案共有________种.(用数字作答)三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数(1)当时,若恒成立,求的最大值;(2)记的解集为集合A,若,求实数的取值范围.18.(12分)在直角坐标系中,曲线的参数方程为(为参数),以坐标原点为极点,以轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为.(1)写出的普通方程和的直角坐标方程;(2)设点在上,点在上,求的最小值以及此时的直角坐标.19.(12分)已知椭圆的离心率为,且过点,点在第一象限,为左顶点,为下顶点,交轴于点,交轴于点.(1)求椭圆的标准方程;(2)若,求点的坐标.20.(12分)已知函数.(1)若函数在上单调递增,求实数的值;(2)定义:若直线与曲线都相切,我们称直线为曲线、的公切线,证明:曲线与总存在公切线.21.(12分)如图,在正四棱柱中,已知,.(1)求异面直线与直线所成的角的大小;(2)求点到平面的距离.22.(10分)已知集合,,,将的所有子集任意排列,得到一个有序集合组,其中.记集合中元素的个数为,,,规定空集中元素的个数为.当时,求的值;利用数学归纳法证明:不论为何值,总存在有序集合组,满足任意,,都有.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】由对数运算法则和等比数列的性质计算.【详解】由题意.故选:D.【点睛】本题考查等比数列的性质,考查对数的运算法则.掌握等比数列的性质是解题关键.2、A【解析】先求得全集包含的元素,由此求得集合的补集.【详解】由解得,故,所以,故选A.【点睛】本小题主要考查补集的概念及运算,考查一元二次不等式的解法,属于基础题.3、B【解析】画出可行域和目标函数,根据平移得到最值点,再利用均值不等式得到答案.【详解】如图所示,...