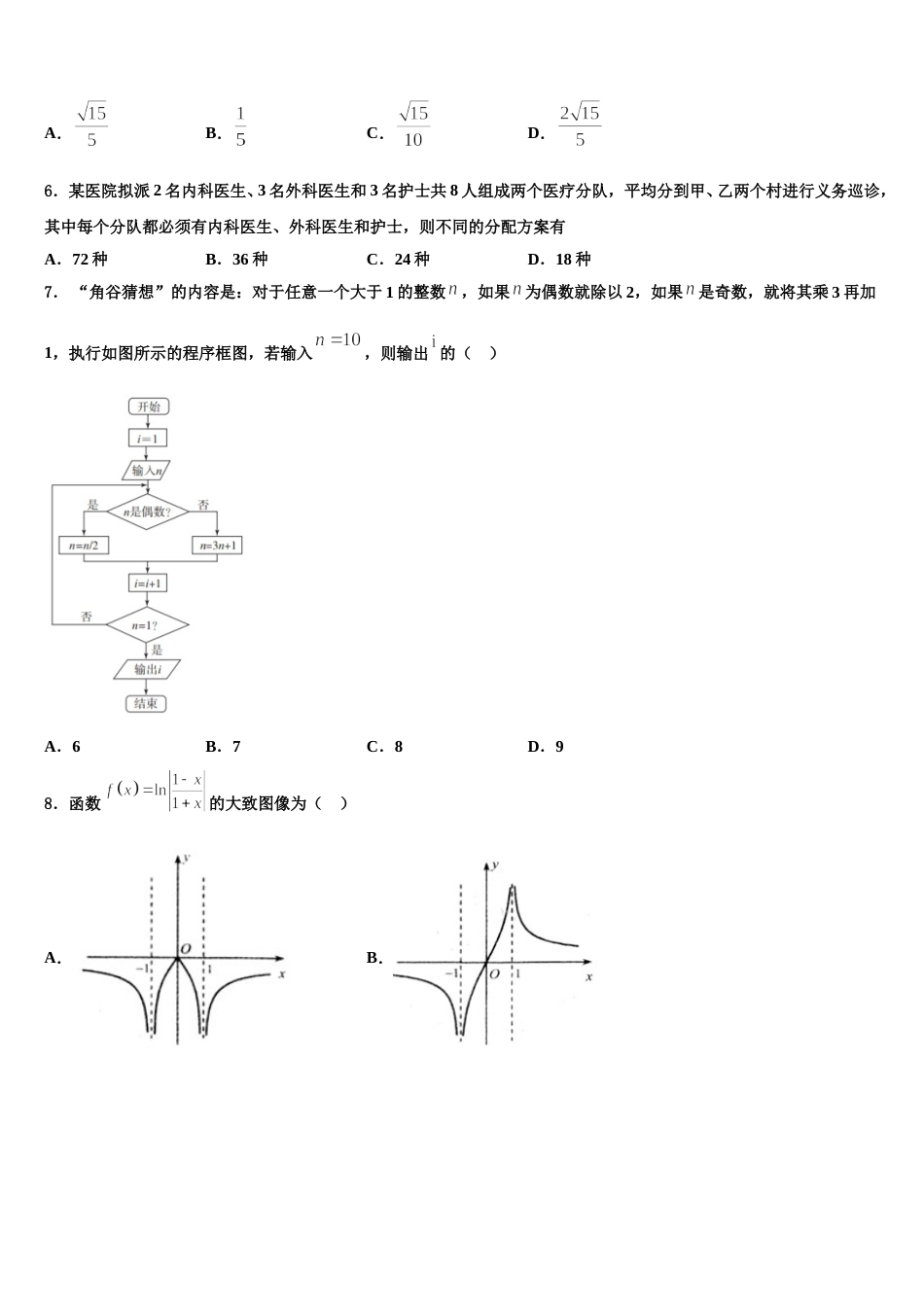
河南省巩义市市直高中 2024 年高三下学期联合考试数学试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.在关于的不等式中,“”是“恒成立”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.公差不为零的等差数列{an}中,a1+a2+a5=13,且 a1、a2、a5成等比数列,则数列{an}的公差等于( )A.1B.2C.3D.43.设函数的定义域为,命题:,的否定是( )A.,B.,C.,D.,4.下列四个结论中正确的个数是(1)对于命题使得,则都有;(2)已知,则 (3)已知回归直线的斜率的估计值是 2,样本点的中心为(4,5),则回归直线方程为;(4)“”是“”的充分不必要条件.A.1B.2C.3D.45.在中,内角 A,B,C 所对的边分别为 a,b,c,D 是 AB 的中点,若,且,则面积的最大值是( )A.B.C.D.6.某医院拟派 2 名内科医生、3 名外科医生和 3 名护士共 8 人组成两个医疗分队,平均分到甲、乙两个村进行义务巡诊,其中每个分队都必须有内科医生、外科医生和护士,则不同的分配方案有A.72 种B.36 种C.24 种D.18 种7. “角谷猜想”的内容是:对于任意一个大于 1 的整数,如果为偶数就除以 2,如果是奇数,就将其乘 3 再加1,执行如图所示的程序框图,若输入,则输出 的( )A.6B.7C.8D.98.函数的大致图像为( )A.B.C.D.9.已知双曲线的左、右顶点分别为,点是双曲线上与不重合的动点,若, 则双曲线的离心率为( )A.B.C.4D.210.已知随机变量的分布列是则( )A.B.C.D.11.对于函数,若满足,则称为函数的一对“线性对称点”.若实数与和与为函数的两对“线性对称点”,则的最大值为( )A.B.C.D.12.如下的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b 分别为 176,320,则输出的 a 为( )A.16B.18C.20D.15二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.设函数在区间上的值域是,则的取值范围是__________.14.函数的定义域为____.15.曲线在处的切线的斜率为________.16.若,则______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)如图 1,已知四边形 BCDE 为直角梯形,,,且,A 为 BE的中点 将沿 AD 折到位置 如图,连结 PC,PB 构成一个四棱锥.(Ⅰ)求证;(Ⅱ)若平面.① 求二面角的大小;② 在棱 PC 上存在点 M,满足,使得直线 AM 与平面 PBC 所成的角为,求的值.18.(12 分)的内角,,的对边分别为,,,其面积记为,满足.(1)求;(2)若,求的值.19.(12 分)每年的寒冷天气都会带热“御寒经济”,以交通业为例,当天气太冷时,不少人都会选择利用手机上的打车软件在网上预约出租车出行,出租车公司的订单数就会增加.下表是某出租车公司从出租车的订单数据中抽取的 5天的日平均气温(单位:℃)与网上预约出租车订单数(单位:份);日平均气温(℃)642网上预约订单数100135150185210(1)经数据分析,一天内平均气温与该出租车公司网约订单数(份)成线性相关关系,试建立关于的回归方程,并预测日平均气温为时,该出租车公司的网约订单数;(2)天气预报未来 5 天有 3 天日平均气温不高于,若把这 5 天的预测数据当成真实的数据,根据表格数据,则从这 5 天中任意选取 2 天,求恰有 1 天网约订单数不低于 210 份的概率.附:回归直线的斜率和截距的最小二乘法估计分别为:20.(12 分)如图,在四棱锥中,侧棱底面,,,,是棱的中点.(1)求证:平面;(2)若,点是线段上一点,且,求直线与平面所成角的正弦值.21.(12 ...