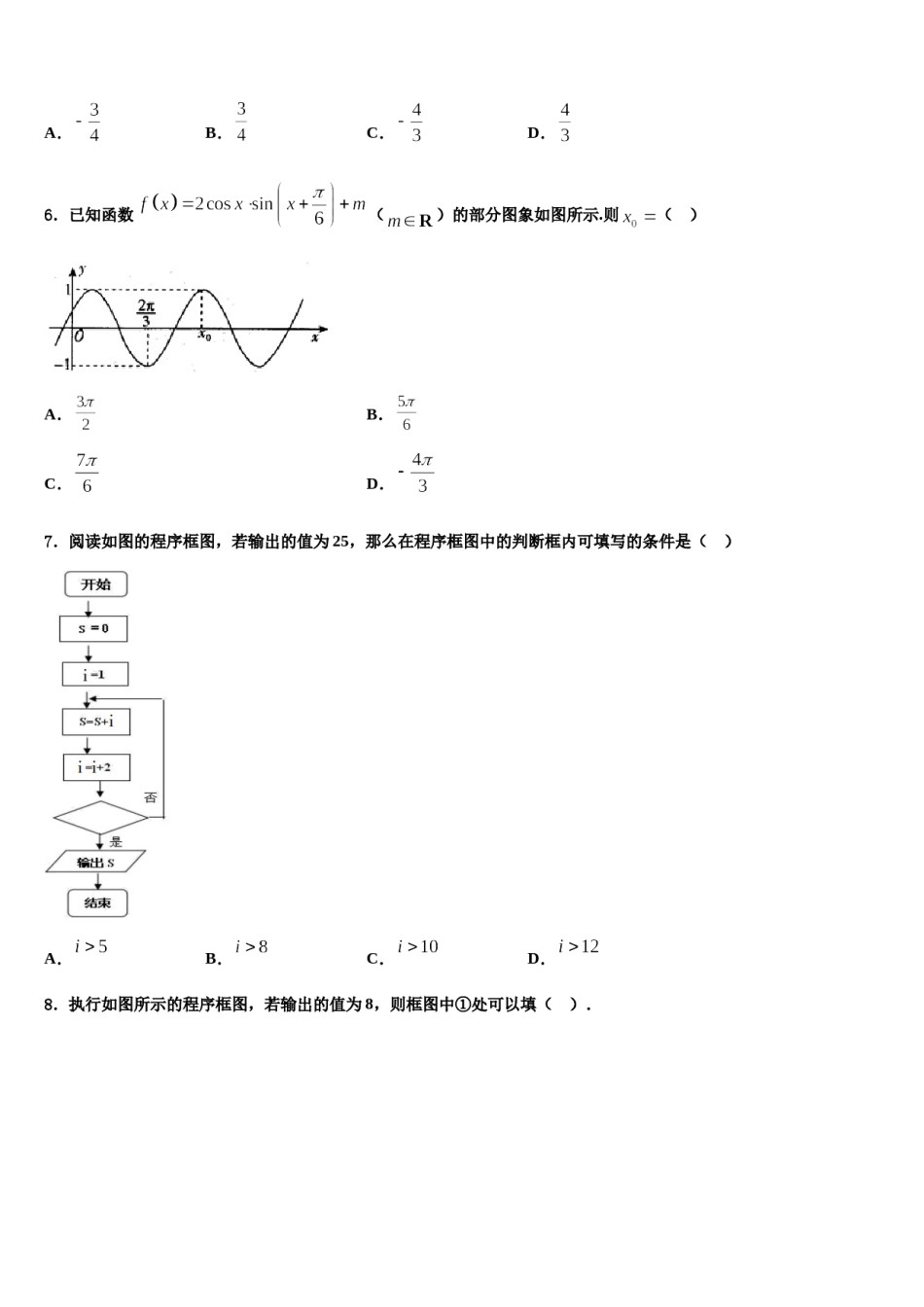
河南省新乡市新乡市第一中学2023-2024学年高三冲刺模拟数学试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知集合,,若,则()A.或B.或C.或D.或2.我国古代数学名著《九章算术》有一问题:“今有鳖臑(biēnaò),下广五尺,无袤;上袤四尺,无广;高七尺.问积几何?”该几何体的三视图如图所示,则此几何体外接球的表面积为()A.平方尺B.平方尺C.平方尺D.平方尺3.我们熟悉的卡通形象“哆啦A梦”的长宽比为.在东方文化中通常称这个比例为“白银比例”,该比例在设计和建筑领域有着广泛的应用.已知某电波塔自下而上依次建有第一展望台和第二展望台,塔顶到塔底的高度与第二展望台到塔底的高度之比,第二展望台到塔底的高度与第一展望台到塔底的高度之比皆等于“白银比例”,若两展望台间高度差为100米,则下列选项中与该塔的实际高度最接近的是()A.400米B.480米C.520米D.600米4.若双曲线的离心率,则该双曲线的焦点到其渐近线的距离为()A.B.2C.D.15.抛物线的准线方程是,则实数()A.B.C.D.6.已知函数()的部分图象如图所示.则()A.B.C.D.7.阅读如图的程序框图,若输出的值为25,那么在程序框图中的判断框内可填写的条件是()A.B.C.D.8.执行如图所示的程序框图,若输出的值为8,则框图中①处可以填().A.B.C.D.9.点为不等式组所表示的平面区域上的动点,则的取值范围是()A.B.C.D.10.已知函数,满足对任意的实数,都有成立,则实数的取值范围为()A.B.C.D.11.复数().A.12.双曲线B.C.D.,那么它的离心率为()的一条渐近线方程为A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.若关于的不等式在上恒成立,则的最大值为__________.14.对于任意的正数,不等式恒成立,则的最大值为_____.15.在中,,,,则________,的面积为________.16.从一箱产品中随机地抽取一件,设事件抽到一等品,事件抽到二等品,事件抽到三等品,且已知,,,则事件“抽到的产品不是一等品”的概率为________三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知在等比数列中,.(1)求数列的通项公式;(2)若,求数列前项的和.18.(12分)中的内角,,的对边分别是,,,若,.(1)求;(2)若,点为边上一点,且,求的面积.19.(12分)设函数.(1)求的值;(2)若,求函数的单调递减区间.20.(12分)已知函数.(1)若,,求函数的单调区间;(2)时,若对一切恒成立,求a的取值范围.21.(12分)已知数列{an}的各项均为正,Sn为数列{an}的前n项和,an2+2an=4Sn+1.(1)求{an}的通项公式;(2)设bn,求数列{bn}的前n项和.22.(10分)在直角坐标系xOy中,直线的参数方程为(t为参数).以原点O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为.的值.(1)写出圆C的直角坐标方程;(2)设直线l与圆C交于A,B两点,,求参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】因为,所以,所以或.若,则,满足.若,解得或.若,则,满足.若,显然不成立,综上或,选B.2、A【解析】根据三视图得出原几何体的立体图是一个三棱锥,将三棱锥补充成一个长方体,此长方体的外接球就是该三棱锥的外接球,由球的表面积公式计算可得选项.【详解】由三视图可得,该几何体是一个如图所示的三棱锥,为三棱锥外接球的球心,此三棱锥的外接球也是此三棱锥所在的长方体的外接球,所以为的中点,设球半径为,则,所以外接球的表面积,故选:A.【点睛】本题考查求几何体的外接球的表面积,关键在于由几何体的三视图得出几何体的立体图,找出外接球的球心位置和半径,属于中档题.3、B【解析】根据题意,画出几何关系,...