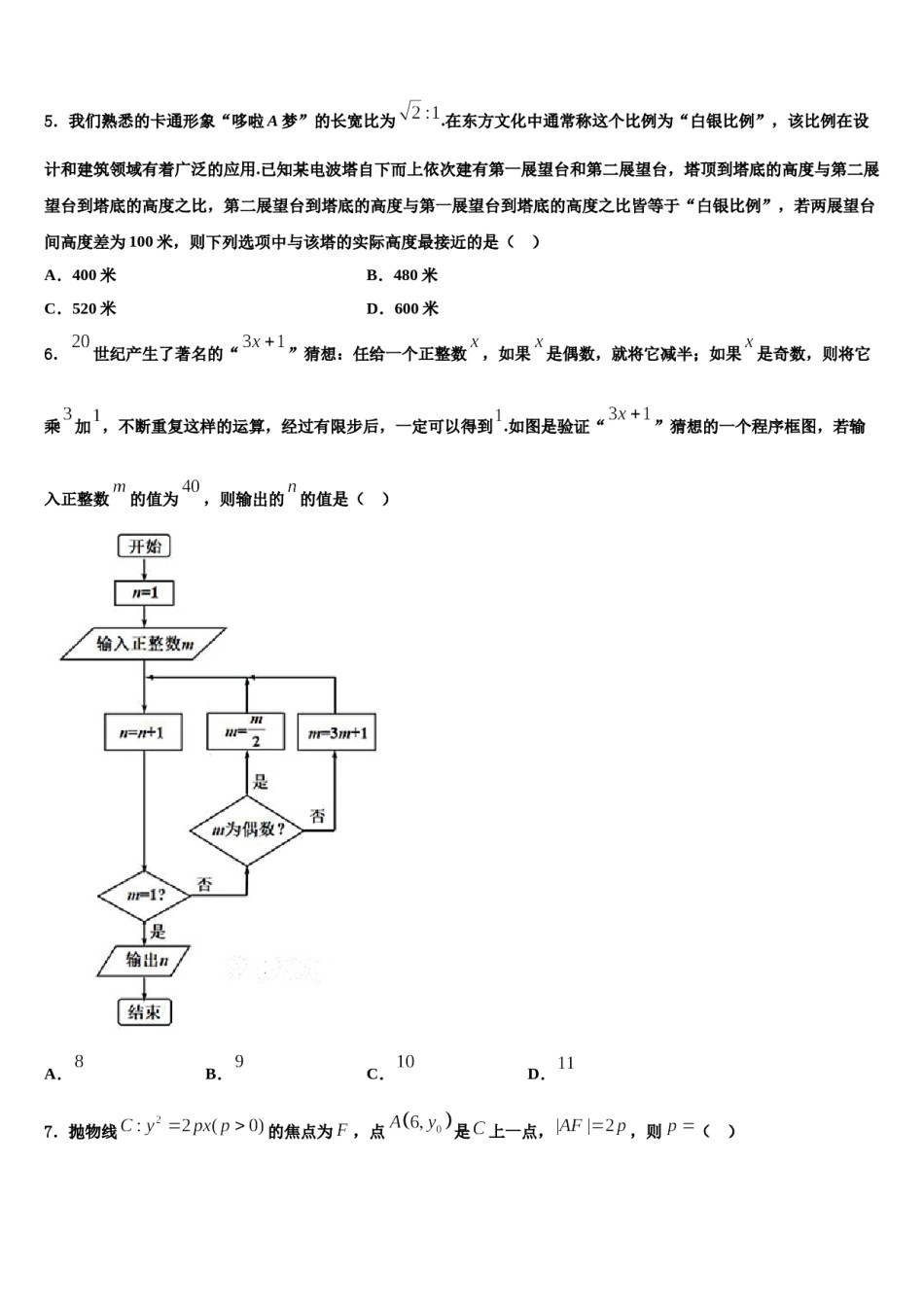
河南省罗山县高级中学2024届高考数学押题试卷注意事项铅笔作答;第二部分必须用黑1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用2B色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知各项都为正的等差数列中,,若,,成等比数列,则()A.B.C.D.2.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上心有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中分别随机选取1个数,则其和等于11的概率是().A.B.C.D.3.已知函数的图像与一条平行于轴的直线有两个交点,其横坐标分别为,则()A.B.C.D.,则等差数列公差()4.已知等差数列的前项和为,若D.4A.2B.C.35.我们熟悉的卡通形象“哆啦A梦”的长宽比为.在东方文化中通常称这个比例为“白银比例”,该比例在设计和建筑领域有着广泛的应用.已知某电波塔自下而上依次建有第一展望台和第二展望台,塔顶到塔底的高度与第二展望台到塔底的高度之比,第二展望台到塔底的高度与第一展望台到塔底的高度之比皆等于“白银比例”,若两展望台间高度差为100米,则下列选项中与该塔的实际高度最接近的是()A.400米B.480米C.520米D.600米6.世纪产生了著名的“”猜想:任给一个正整数,如果是偶数,就将它减半;如果是奇数,则将它乘加,不断重复这样的运算,经过有限步后,一定可以得到.如图是验证“”猜想的一个程序框图,若输入正整数的值为,则输出的的值是()A.B.C.D.7.抛物线是上一点,的焦点为,点,则()A.B.C.D.8.已知,其中是虚数单位,则对应的点的坐标为()A.B.C.D.9.若函数的图象向右平移个单位长度得到函数的图象,若函数在区间上单调递增,则的最大值为().A.B.C.D.10.已知函数的图象与直线的相邻交点间的距离为,若定义,则函数,在区间内的图象是()A.B.C.D.11.关于函数,有下列三个结论:①是的一个周期;②在上单调递增;③的值域为.则上述结论中,正确的个数为()A.B.C.D.12.已知直线:过双曲线的一个焦点且与其中一条渐近线平行,则双曲线的方程为()A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。13.函数在上的最小值和最大值分别是_____________.14.直线xsinα+y+2=0的倾斜角的取值范围是________________..为了便于管理,在线段15.如图,养殖公司欲在某湖边依托互相垂直的湖岸线、围成一个三角形养殖区之间有一观察站点,到直线,的距离分别为8百米、1百米,则观察点到点、距离之和的最小值为______________百米.16.割圆术是估算圆周率的科学方法,由三国时期数学家刘徽创立,他用圆内接正多边形面积无限逼近圆面积,从而得出圆周率.现在半径为1的圆内任取一点,则该点取自其内接正十二边形内部的概率为________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)设的内角的对边分别为,已知.(1)求;(2)若为锐角三角形,求的取值范围.18.(12分)已知函数的最大值为,其中.(1)求实数的值;(2)若求证:.19.(12分)在数列中,,(1)求数列的通项公式;(2)若存在,使得成立,求实数的最小值20.(12分)已知抛物线上一点到焦点的距离为2,(1)求的值与抛物线的方程;(2)抛物线上第一象限内的动点在点右侧,抛物线上第四象限内的动点,满足,求直线的斜率范围.21.(12分)等差数列的前项和为,已知,.(1)求数列的通项公式;(2)设数列{}的前项和为,求使成立的的最小值.22.(10分)在中,角所对的边分别是,且.(1)求角的大小;(2)若,求边长.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、A【解析】试题分析:设公差为或(舍),故选A.考点:等差数列及其性质.2、A【解析】基本事件总...