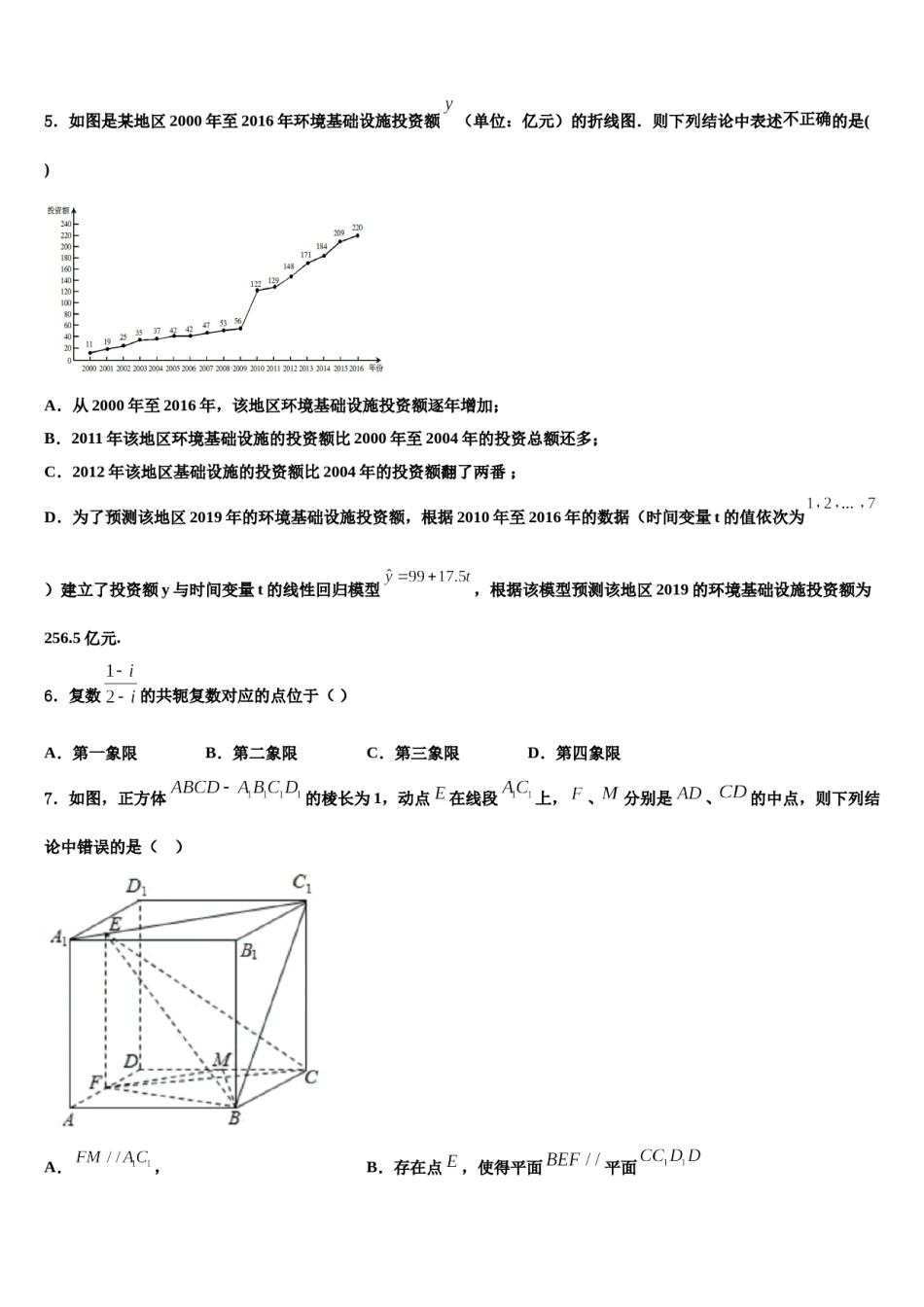
浙江省宁波市2024届高考压轴卷数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数的最大值为,若存在实数,使得对任意实数总有成立,则的最小值为()A.B.C.D.2.若双曲线:的一条渐近线方程为,则()A.B.C.D.3.如图所示,网格纸上小正方形的边长为,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为()A.B.C.D.4.已知函数A.,若不等式对任意的恒成立,则实数k的取值范围是()B.C.D.5.如图是某地区2000年至2016年环境基础设施投资额(单位:亿元)的折线图.则下列结论中表述不正确的是()A.从2000年至2016年,该地区环境基础设施投资额逐年增加;B.2011年该地区环境基础设施的投资额比2000年至2004年的投资总额还多;C.2012年该地区基础设施的投资额比2004年的投资额翻了两番;D.为了预测该地区2019年的环境基础设施投资额,根据2010年至2016年的数据(时间变量t的值依次为)建立了投资额y与时间变量t的线性回归模型,根据该模型预测该地区2019的环境基础设施投资额为256.5亿元.6.复数的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限7.如图,正方体的棱长为1,动点在线段上,、分别是、的中点,则下列结论中错误的是()A.,B.存在点,使得平面平面C.平面D.三棱锥的体积为定值8.已知等差数列中,则()A.109.已知直线:B.16C.20D.24与圆:交于,两点,与平行的直线与圆交于,两点,且与的面积相等,给出下列直线:①,②,③,④.其中满足条件的所有直线的编号有()A.①②B.①④C.②③D.①②④10.如图,圆锥底面半径为,体积为,、是底面圆的两条互相垂直的直径,是母线的中点,已知过与的平面与圆锥侧面的交线是以为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点的距离等于()A.B.1C.D.11.集合的子集的个数是()A.212.空气质量指数B.3C.4D.8是反映空气状况的指数,指数值趋小,表明空气质量越好,下图是某市10月1日-20日指数变化趋势,下列叙述错误的是()A.这20天中指数值的中位数略高于100B.这20天中的中度污染及以上(指数)的天数占C.该市10月的前半个月的空气质量越来越好D.总体来说,该市10月上旬的空气质量比中旬的空气质量好二、填空题:本题共4小题,每小题5分,共20分。13.某几何体的三视图如图所示(单位:),则该几何体的表面积是______,体积是_____.14.已知集合,则_______.15.已知,(,),则=_______.16.在中,内角所对的边分别为,若,的面积为,则_______,_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数,.(1)若不等式对恒成立,求的最小值;(2)证明:.(3)设方程的实根为.令若存在,,,使得,证明:.18.(12分)一种游戏的规则为抛掷一枚硬币,每次正面向上得2分,反面向上得1分.(1)设抛掷4次的得分为,求变量的分布列和数学期望.(2)当游戏得分为时,游戏停止,记得分的概率和为.①求;②当时,记,证明:数列为常数列,数列为等比数列.19.(12分)在中,内角的边长分别为,且.(1)若,,求的值;(2)若,且的面积,求和的值.20.(12分)等差数列中,.(1)求的通项公式;(2)设,记为数列前项的和,若,求.21.(12分)2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品的研发费用(百万元)和销量(万盒)的统计数据如下:2361013151821研发费用(百万元)销量(万盒)1122.53.53.54.56(1)求与的相关系数精确到0.01,并判断与的关系是否可用线性回归方程模型拟合...