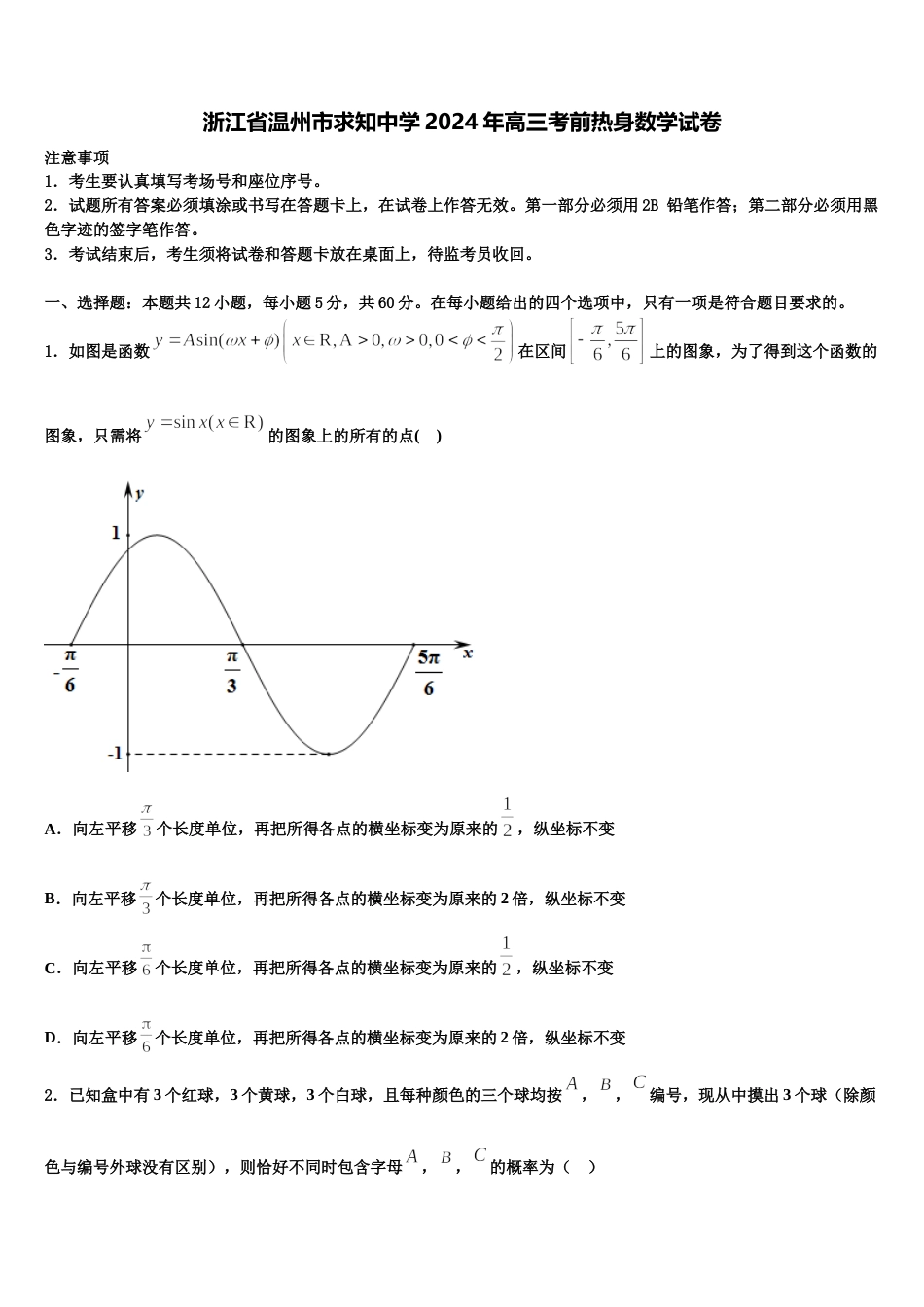
浙江省温州市求知中学 2024 年高三考前热身数学试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.如图是函数在区间上的图象,为了得到这个函数的图象,只需将的图象上的所有的点( )A.向左平移个长度单位,再把所得各点的横坐标变为原来的,纵坐标不变B.向左平移个长度单位,再把所得各点的横坐标变为原来的 2 倍,纵坐标不变C.向左平移个长度单位,再把所得各点的横坐标变为原来的,纵坐标不变D.向左平移个长度单位,再把所得各点的横坐标变为原来的 2 倍,纵坐标不变2.已知盒中有 3 个红球,3 个黄球,3 个白球,且每种颜色的三个球均按,,编号,现从中摸出 3 个球(除颜色与编号外球没有区别),则恰好不同时包含字母,,的概率为( )A.B.C.D.3.设向量,满足,,,则的取值范围是A.B.C.D.4.若复数,其中 为虚数单位,则下列结论正确的是( )A.的虚部为B.C.的共轭复数为D.为纯虚数5.设集合 A={4,5,7,9},B={3,4,7,8,9},全集 U=AB,则集合中的元素共有 ( )A.3 个B.4 个C.5 个D.6 个6.若函数有且只有 4 个不同的零点,则实数的取值范围是( )A.B.C.D.7.的图象如图所示,,若将的图象向左平移个单位长度后所得图象与的图象重合,则可取的值的是( )A.B.C.D.8.已知等差数列的公差不为零,且,,构成新的等差数列,为的前项和,若存在使得,则( )A.10B.11C.12D.139.已知函数,则函数的零点所在区间为( )A.B.C.D.10.已知,,,则( )A.B.C.D.11.我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸;③台体的体积公式).A.2 寸B.3 寸C.4 寸D.5 寸12.△ABC 中,AB=3,,AC=4,则△ABC 的面积是( )A.B.C.3D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知,椭圆的方程为,双曲线方程为,与的离心率之积为,则的渐近线方程为________.14.高三(1)班共有 56 人,学号依次为 1,2,3,…,56,现用系统抽样的办法抽取一个容量为 4 的样本,已知学号为 6,34,48 的同学在样本中,那么还有一个同学的学号应为 .15.已知函数,则曲线在处的切线斜率为________.16.袋中装有两个红球、三个白球,四个黄球,从中任取四个球,则其中三种颜色的球均有的概率为________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知动圆 Q 经过定点,且与定直线相切(其中 a 为常数,且).记动圆圆心 Q的轨迹为曲线 C.(1)求 C 的方程,并说明 C 是什么曲线?(2)设点 P 的坐标为,过点 P 作曲线 C 的切线,切点为 A,若过点 P 的直线 m 与曲线 C 交于 M,N 两点,则是否存在直线 m,使得?若存在,求出直线 m 斜率的取值范围;若不存在,请说明理由.18.(12 分)已知椭圆()的半焦距为,原点到经过两点,的直线的距离为.(Ⅰ)求椭圆的离心率;(Ⅱ)如图,是圆的一条直径,若椭圆经过,两点,求椭圆的方程.19.(12 分)已知都是大于零的实数.(1)证明;(2)若,证明.20.(12 分)贫困人口全面脱贫是全面建成小康社会的标志性指标.党的十九届四中全会提出“坚决打赢脱贫攻坚战,建立解决相对贫困的长效机制”对当前和下一个阶段的扶贫工作进行了前瞻性的部署,即 2020 年要通过精准扶贫全面消除绝对贫困,实现全面建成小康社会的奋斗目标.为了响应党的号召,某市对口某贫困乡镇开展扶贫工作.对某种农产品加工生产销售进行指导,经...