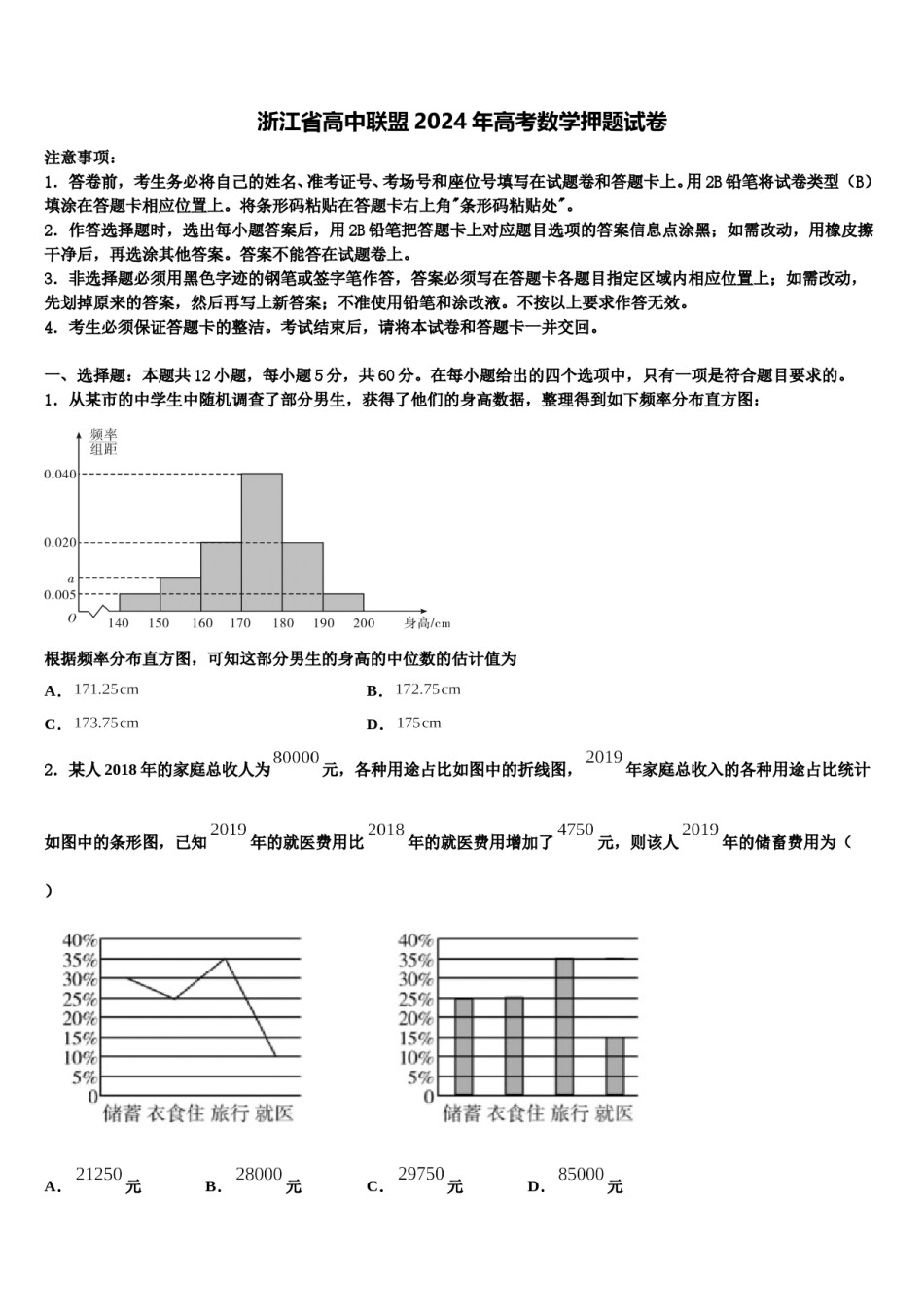
浙江省高中联盟2024年高考数学押题试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图:根据频率分布直方图,可知这部分男生的身高的中位数的估计值为A.B.C.D.2.某人2018年的家庭总收人为元,各种用途占比如图中的折线图,年家庭总收入的各种用途占比统计如图中的条形图,已知年的就医费用比年的就医费用增加了元,则该人年的储畜费用为()A.元B.元C.元D.元3.已知,,由程序框图输出的为()A.1B.0C.D.4.复数的虚部为()A.B.C.2D.5.已知函数是定义在上的偶函数,当时,,则,,的大小关系为()A.B.C.D.6.我国宋代数学家秦九韶(1202-1261)在《数书九章》(1247)一书中提出“三斜求积术”,即:以少广求之,以小斜幂并大斜幂减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂减上,余四约之,为实;一为从隅,开平方得积.其实质是根据三角形的三边长,,求三角形面积,即.若的面积,,,则等于()A.B.C.或D.或7.已知是两条不重合的直线,是两个不重合的平面,下列命题正确的是()A.若,,,,则B.若,,,则C.若,,,则D.若,,,则8.设全集,集合,,则集合()A.B.C.D.9.设为虚数单位,则复数在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限10.上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:黄赤交角正切值0.4390.4440.4500.4550.461公元前8000年年代公元元年公元前2000年公元前4000年公元前6000年根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是()A.公元前2000年到公元元年B.公元前4000年到公元前2000年C.公元前6000年到公元前4000年D.早于公元前6000年11.已知将函数(,)的图象向右平移个单位长度后得到函数的图象,若和的图象都关于对称,则下述四个结论:①②③④点为函数的一个对称中心其中所有正确结论的编号是()A.①②③B.①③④C.①②④D.②③④12.直线l过抛物线的焦点且与抛物线交于A,B两点,则的最小值是A.10B.9C.8D.7二、填空题:本题共4小题,每小题5分,共20分。13.在的展开式中,各项系数之和为,则展开式中的常数项为__________________.14.“”是“”的__________条件.(填写“充分必要”、“充分不必要”、“必要不充分”、“既不充分也不必要”之一)15.展开式中项系数为160,则的值为______.16.曲线在点处的切线方程为______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)如图所示的几何体中,,四边形为正方形,四边形为梯形,,,,为中点.(1)证明:;(2)求二面角的余弦值.18.(12分)在△ABC中,分别为三个内角A、B、C的对边,且(1)求角A;且求△ABC的面积.(2)若19.(12分)已知函数,其中.(Ⅰ)若,求函数的单调区间;(Ⅱ)设.若在上恒成立,求实数...