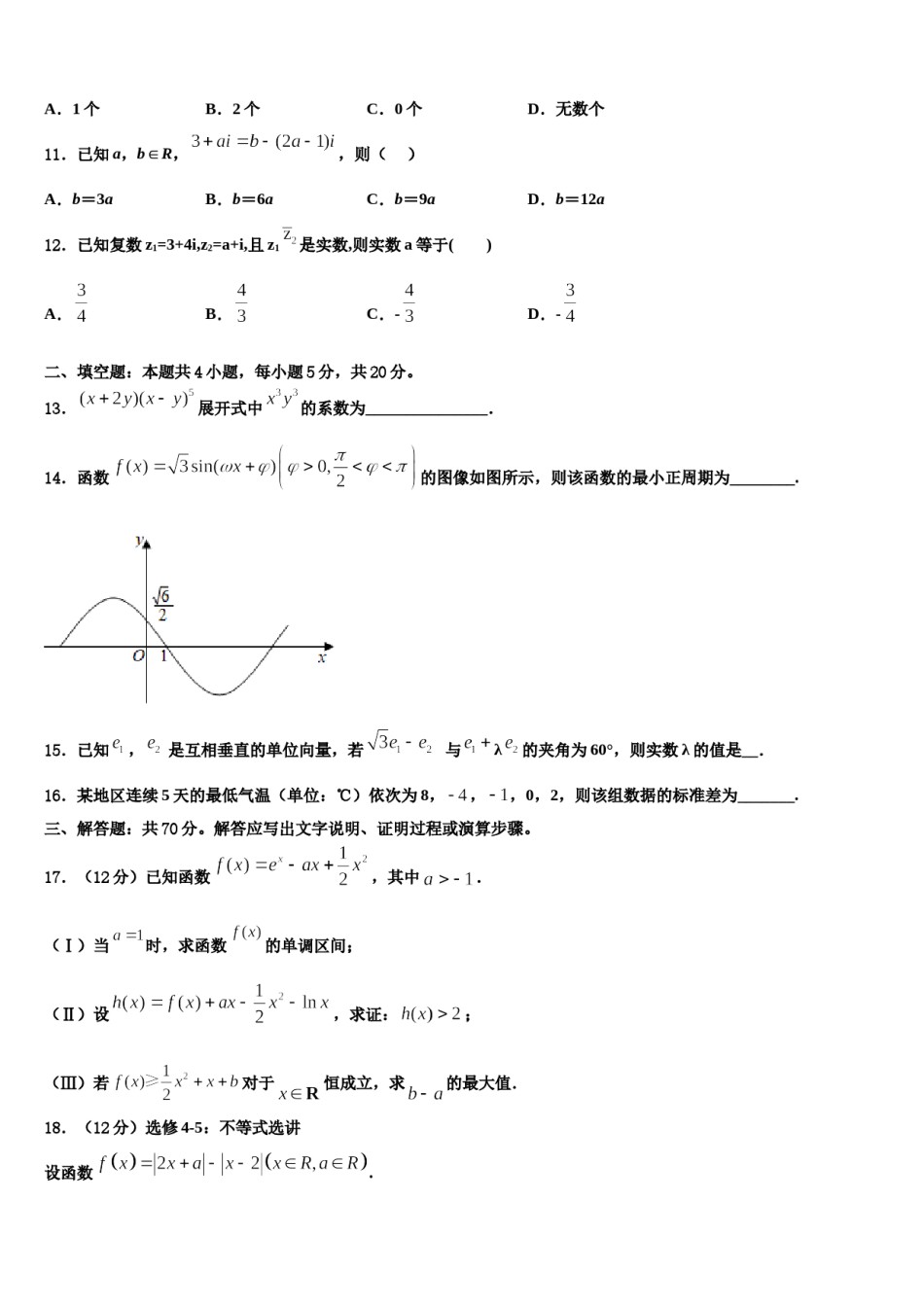
温州市22中2023-2024学年高三下第一次测试数学试题请考生注意:1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知函数,,,,则,,的大小关系为()A.B.C.D.2.甲乙两人有三个不同的学习小组,,可以参加,若每人必须参加并且仅能参加一个学习小组,则两人参加同一个小组的概率为()A.B.C.D.3.已知函数是定义在上的偶函数,当时,,则,,的大小关系为()A.B.C.D.4.数列满足:,则数列前项的和为A.B.C.D.5.盒子中有编号为1,2,3,4,5,6,7的7个相同的球,从中任取3个编号不同的球,则取的3个球的编号的中位数恰好为5的概率是()A.B.C.D.6.若复数满足,则的虚部为()A.5B.C.D.-57.百年双中的校训是“仁”、“智”、“雅”、“和”.在2019年5月18日的高三趣味运动会中有这样的一个小游戏.袋子中有大小、形状完全相同的四个小球,分别写有“仁”、“智”、“雅”、“和”四个字,有放回地从中任意摸出一个小球,直到“仁”、“智”两个字都摸到就停止摸球.小明同学用随机模拟的方法恰好在第三次停止摸球的概率.利用电脑随机产生1到4之间(含1和4)取整数值的随机数,分别用1,2,3,4代表“仁”、“智”、“雅”、“和”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下20组随机数:141432341342234142243331112322342241244431233214344142134412由此可以估计,恰好第三次就停止摸球的概率为()A.B.C.D.8.已知集合,将集合的所有元素从小到大一次排列构成一个新数列,则()D.1095A.1194B.1695C.3119.函数()的图象的大致形状是()A.B.C.D.10.抛物线的焦点为,则经过点与点且与抛物线的准线相切的圆的个数有()A.1个B.2个C.0个D.无数个D.b=12a11.已知a,b∈R,,则()A.b=3aB.b=6aC.b=9a12.已知复数z1=3+4i,z2=a+i,且z1是实数,则实数a等于()A.B.C.-D.-二、填空题:本题共4小题,每小题5分,共20分。13.展开式中的系数为_______________.14.函数的图像如图所示,则该函数的最小正周期为________.15.已知,是互相垂直的单位向量,若与λ的夹角为60°,则实数λ的值是__.16.某地区连续5天的最低气温(单位:℃)依次为8,,,0,2,则该组数据的标准差为_______.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知函数,其中.(Ⅰ)当时,求函数的单调区间;(Ⅱ)设,求证:;(Ⅲ)若对于恒成立,求的最大值.18.(12分)选修4-5:不等式选讲设函数.(1)当时,求不等式的解集;(2)若在上恒成立,求实数的取值范围.19.(12分)中的内角,,的对边分别是,,,若,.,线段的中(1)求;(2)若,点为边上一点,且,求的面积.20.(12分)如图,在中,角的对边分别为,且满足点为.(Ⅰ)求角的大小;(Ⅱ)已知,求的大小.21.(12分)选修4—5;不等式选讲.已知函数.(1)若的解集非空,求实数的取值范围;(2)若正数满足,为(1)中m可取到的最大值,求证:.22.(10分)已知函数.(1)当时.处的切线方程;①求函数在②定义其中,求;(2)当时,设,(为自然对数的底数),若对任意给定的,在上总存在两个不同的,使得成立,求的取值范围.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】可判断函数在上单调递增,且,所以.【详解】在上单调递增,且,所以.故选:B【点睛】本题主要考查了函数单调性的判定,指数函数与对数函数的性质,利用单调性比大小等知识,考查了学生的运算求解能力.2、A【解析】依题意,基本事件的总数有种,两个人参加同一个小组,方法数有种,故概率为.3、C【解析】根据函数的奇偶性得,再比较的大小,根据函数的单调性可得选项.【详解】依题意...