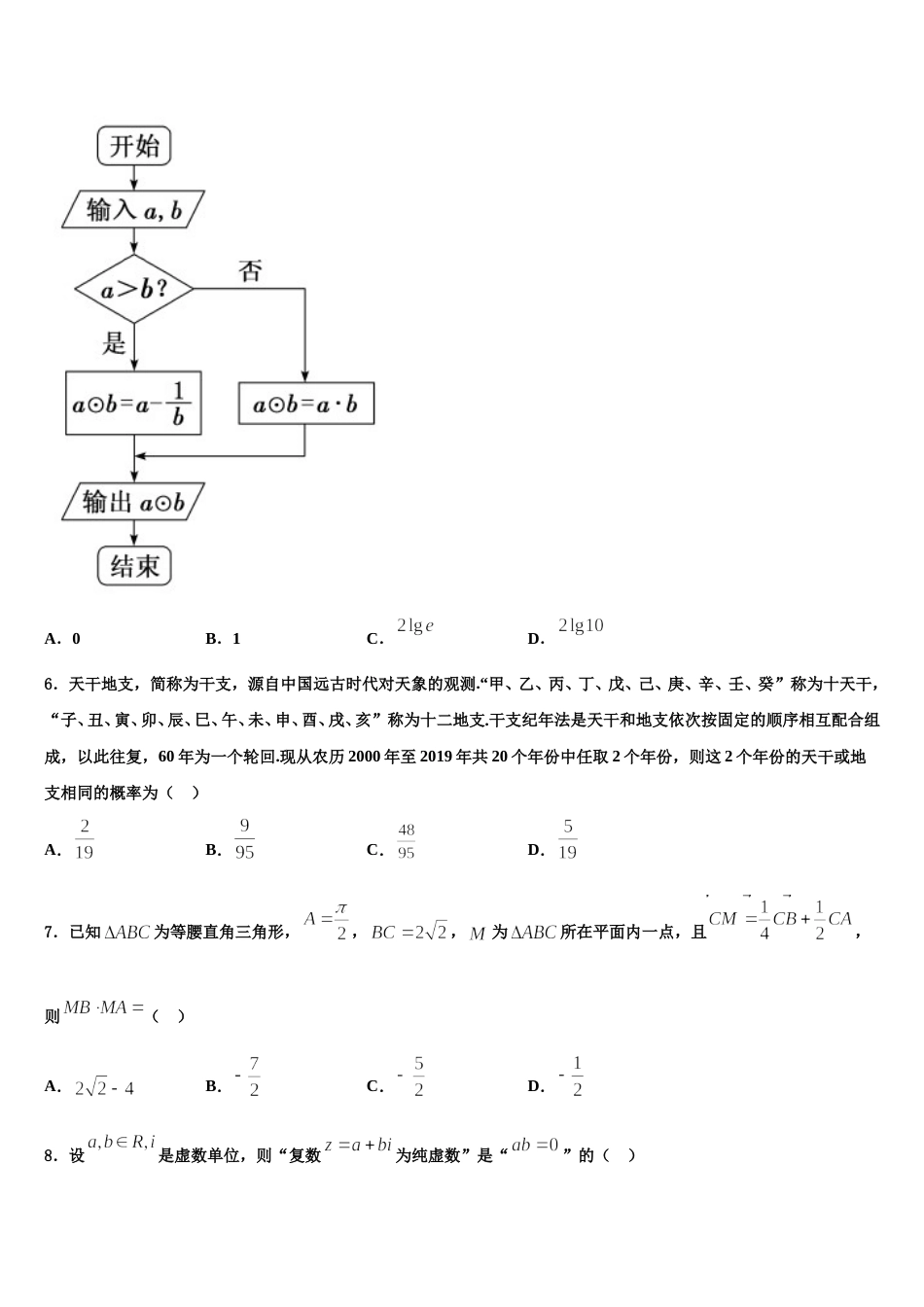
湖北省武汉市常青一中 2023-2024 学年高考数学押题试卷注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.设函数若关于的方程有四个实数解,其中,则的取值范围是( )A.B.C.D.2.已知集合,,则等于( )A.B.C.D.3.已知复数为纯虚数( 为虚数单位),则实数( )A.-1B.1C.0D.24.在中,为中点,且,若,则( )A.B.C.D.5.执行如图所示的程序框图,若输入,,则输出的值为( )A.0B.1C.D.6.天干地支,简称为干支,源自中国远古时代对天象的观测.“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”称为十天干,“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”称为十二地支.干支纪年法是天干和地支依次按固定的顺序相互配合组成,以此往复,60 年为一个轮回.现从农历 2000 年至 2019 年共 20 个年份中任取 2 个年份,则这 2 个年份的天干或地支相同的概率为( )A.B.C.D.7.已知为等腰直角三角形,,,为所在平面内一点,且,则( )A.B.C.D.8.设是虚数单位,则“复数为纯虚数”是“”的( )A.充要条件B.必要不充分条件C.既不充分也不必要条件D.充分不必要条件9.已知函数是上的偶函数,且当时,函数是单调递减函数,则,,的大小关系是( )A.B.C.D.10.集合中含有的元素个数为( )A.4B.6C.8D.1211.刘徽是我国魏晋时期伟大的数学家,他在《九章算术》中对勾股定理的证明如图所示.“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也.合成弦方之幂,开方除之,即弦也”.已知图中网格纸上小正方形的边长为 1,其中“正方形为朱方,正方形为青方”,则在五边形内随机取一个点,此点取自朱方的概率为( )A.B.C.D.12.设为锐角,若,则的值为( )A.B. C. D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.从编号为 ,,,的张卡片中随机抽取一张,放回后再随机抽取一张,则第二次抽得的卡片上的数字能被第一次抽得的卡片上数字整除的概率为_____________.14.二项式的展开式的各项系数之和为_____,含项的系数为_____.15.在正方体中,已知点在直线上运动,则下列四个命题中:①三棱锥的体积不变;②;③当为中点时,二面角 的余弦值为;④若正方体的棱长为 2,则的最小值为;其中说法正确的是____________(写出所有说法正确的编号)16.已知一个正四棱锥的侧棱与底面所成的角为,侧面积为,则该棱锥的体积为__________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)在锐角三角形中,角的对边分别为.已知成等差数列,成等比数列.(1)求的值;(2)若的面积为求的值.18.(12 分)已知函数,其中.(Ⅰ)当时,求函数的单调区间;(Ⅱ)设,求证:;(Ⅲ)若对于恒成立,求的最大值.19.(12 分)如图,在四棱锥中,侧棱底面,,,,,是棱中点.(1)已知点在棱上,且平面平面,试确定点的位置并说明理由;(2)设点是线段上的动点,当点在何处时,直线与平面所成角最大?并求最大角的正弦值.20.(12 分)已知二阶矩阵,矩阵 属于特征值的一个特征向量为,属于特征值的一个特征向量为.求矩阵 .21.(12 分)已知椭圆的左右焦点分别为,焦距为 4,且椭圆过点,过点且不平行于坐标轴的直线 交椭圆与两点,点关于轴的对称点为,直线交轴于点.(1)求的周长;(2)求面积的最大值.22.(10 分)已知椭圆的右焦点为,过点且与轴垂直的直线被椭圆截得的线段长为,且与短轴两端点的连线相互垂直.(1)求椭圆的方程;(2)若圆上存在两点,,椭圆上存在两个点满足:三点共线,三点共线,且,求四边形面积的取值范围.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出...