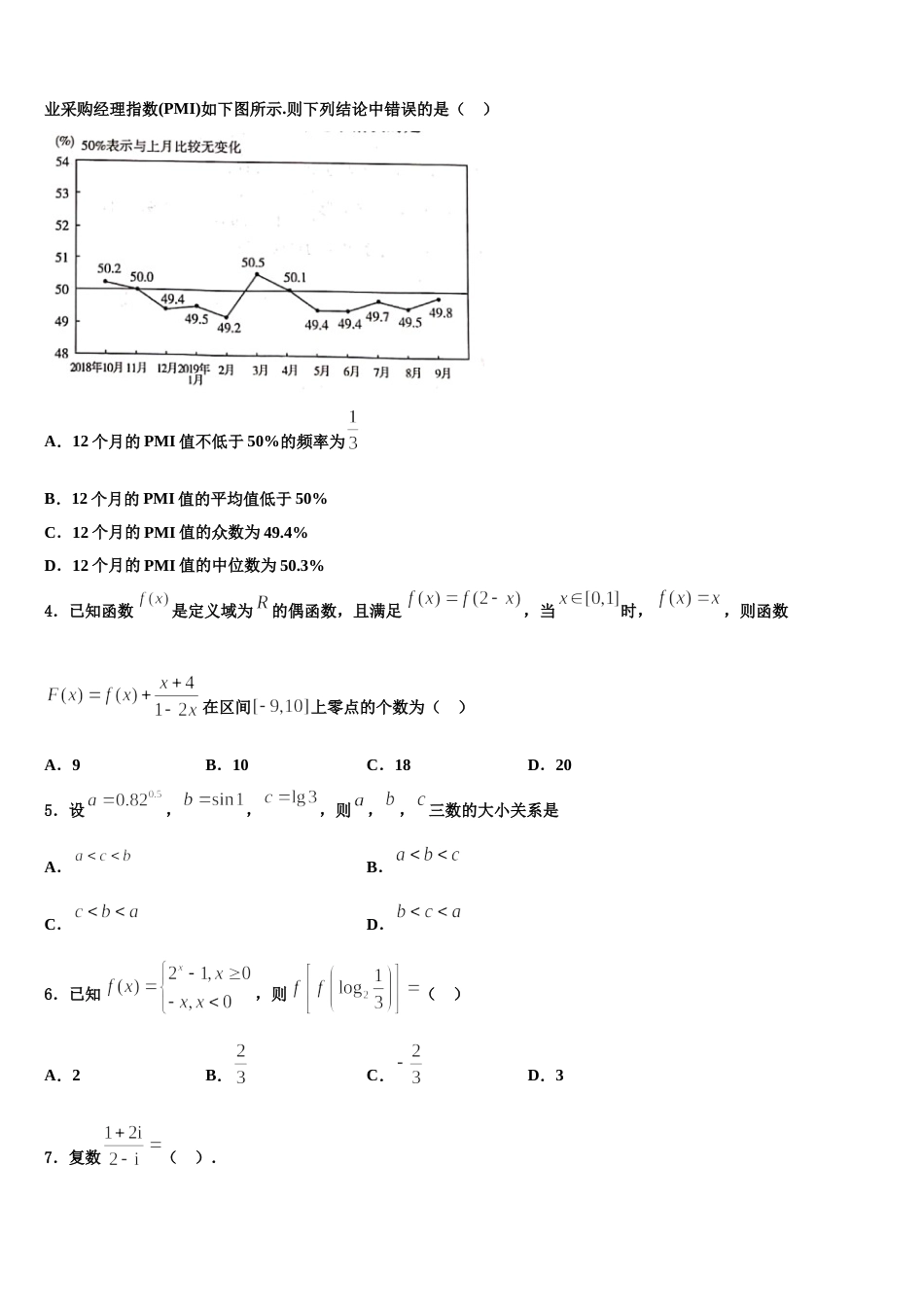
湖南省十四校 2024 届高三下学期联考数学试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.某学校调查了 200 名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是 17.5,30],样本数据分组为 17.5,20),20,22.5),22.5,25),25,27.5),27.5,30).根据直方图,这200 名学生中每周的自习时间不少于 22.5 小时的人数是( )A.56B.60C.140D.1202.明代数学家程大位(1533~1606 年),有感于当时筹算方法的不便,用其毕生心血写出《算法统宗》,可谓集成计算的鼻祖.如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题.执行该程序框图,若输出的的值为,则输入的的值为( )A.B.C.D.3.国家统计局服务业调查中心和中国物流与采购联合会发布的 2018 年 10 月份至 2019 年 9 月份共 12 个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )A.12 个月的 PMI 值不低于 50%的频率为B.12 个月的 PMI 值的平均值低于 50%C.12 个月的 PMI 值的众数为 49.4%D.12 个月的 PMI 值的中位数为 50.3%4.已知函数是定义域为的偶函数,且满足,当时,,则函数在区间上零点的个数为( )A.9B.10C.18D.205.设,,,则,,三数的大小关系是A.B.C.D.6.已知,则( )A.2B.C.D.37.复数( ).A.B.C.D.8.设直线 过点,且与圆:相切于点,那么( )A.B.3C.D.19.如图,平面四边形中,,,,为等边三角形,现将沿翻折,使点移动至点,且,则三棱锥的外接球的表面积为( )A.B.C.D.10.将函数的图象分别向右平移个单位长度与向左平移(>0)个单位长度,若所得到的两个图象重合,则的最小值为( )A.B.C.D.11.如图,在正四棱柱中,,分别为的中点,异面直线与所成角的余弦值为,则( )A.直线与直线异面,且B.直线与直线共面,且C.直线与直线异面,且D.直线与直线共面,且12.如图所示,正方体 ABCD-A1B1C1D1的棱长为 1,线段 B1D1上有两个动点 E、F 且 EF=,则下列结论中错误的是( )A.AC⊥BEB.EF平面 ABCDC.三棱锥 A-BEF 的体积为定值D.异面直线 AE,BF 所成的角为定值二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.若,则____.14.函数的定义域是___________.15.已知向量,,则______.16.在中,已知,则的最小值是________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知,,分别是三个内角,,的对边,.(1)求;(2)若,,求,.18.(12 分)在直角坐标系中,直线 的参数方程为( 为参数).以坐标原点为极点,轴正半轴为极轴建立极坐标系,圆的极坐标方程为.(1)求直线 和圆的普通方程;(2)已知直线 上一点,若直线 与圆交于不同两点,求的取值范围.19.(12 分)为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据得到如图所示的频率分布直方图,若尺寸落在区间之外,则认为该零件属“不合格”的零件,其中,s 分别为样本平均数和样本标准差,计算可得(同一组中的数据用该组区间的中点值作代表).(1)求样本平均数的大小;(2)若一个零件的尺寸是 100 cm,试判断该零件是否属于“不合格”的零件.20.(12 分)在直角坐标系中,曲线的参数方程为( 为参数,),点.以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)求曲线的直角坐标方程,并指出其形状;(2)曲线与曲线交于,两点,若,求的值.21.(12 分)如图,在平面直角坐标系 xOy 中,已知椭圆的离心率为,以椭圆 C 左顶点 T ...