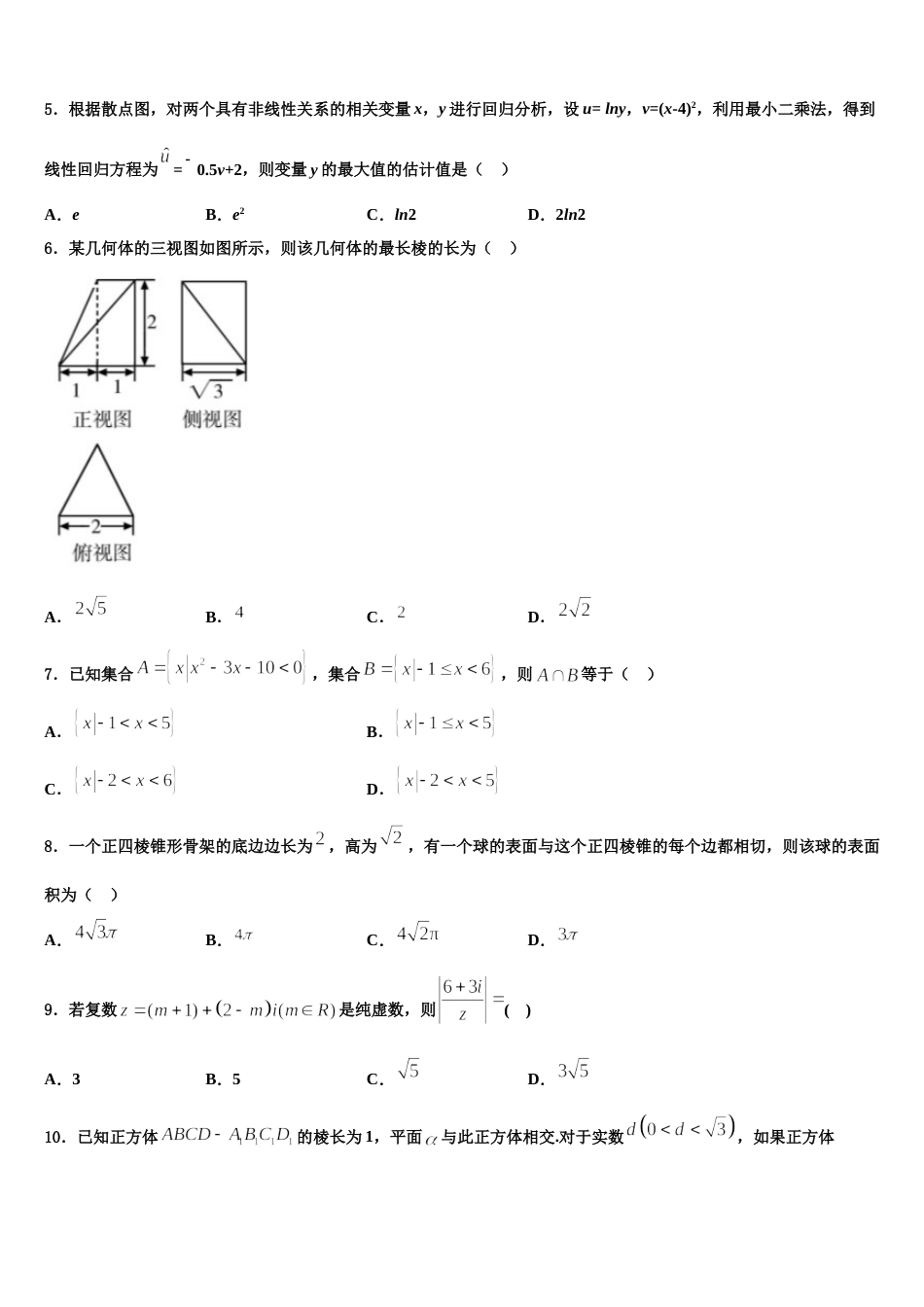
湖南省岳阳市临湘市 2024 年高三第二次联考数学试卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知 a,b 是两条不同的直线,α,β 是两个不同的平面,且,,则“”是“”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.设 m,n 为直线,、为平面,则的一个充分条件可以是( )A.,,B.,C.,D.,3.若双曲线的焦距为,则的一个焦点到一条渐近线的距离为( )A.B.C.D.4.执行如图所示的程序框图,若输出的,则输入的整数的最大值为( )A.7B.15C.31D.635.根据散点图,对两个具有非线性关系的相关变量 x,y 进行回归分析,设 u= lny,v=(x-4)2,利用最小二乘法,得到线性回归方程为=0.5v+2,则变量 y 的最大值的估计值是( )A.eB.e2C.ln2D.2ln26.某几何体的三视图如图所示,则该几何体的最长棱的长为( )A.B.C.D.7.已知集合,集合,则等于( )A.B.C.D.8.一个正四棱锥形骨架的底边边长为,高为,有一个球的表面与这个正四棱锥的每个边都相切,则该球的表面积为( )A.B.C.D.9.若复数是纯虚数,则( )A.3B.5C.D.10.已知正方体的棱长为 1,平面与此正方体相交.对于实数,如果正方体的八个顶点中恰好有个点到平面的距离等于,那么下列结论中,一定正确的是A.B.C.D.11.要得到函数的图象,只需将函数图象上所有点的横坐标( )A.伸长到原来的 2 倍(纵坐标不变),再将得到的图象向右平移个单位长度B.伸长到原来的 2 倍(纵坐标不变),再将得到的图像向左平移个单位长度C.缩短到原来的倍(纵坐标不变),再将得到的图象向左平移个单位长度D.缩短到原来的倍(纵坐标不变),再将得到的图象向右平移个单位长度12.设函数在定义城内可导,的图象如图所示,则导函数的图象可能为( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知向量,,若,则________.14.已知函数,若,则___________.15.设是公差不为 0 的等差数列的前项和,且,则______.16.函数在上的最小值和最大值分别是_____________.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知顶点是坐标原点的抛物线的焦点在轴正半轴上,圆心在直线上的圆与轴相切,且关于点对称.(1)求和的标准方程;(2)过点的直线 与交于,与交于,求证:.18.(12 分)已知分别是内角的对边,满足(1)求内角的大小(2)已知,设点是外一点,且,求平面四边形面积的最大值.19.(12 分)△ABC 的内角的对边分别为,已知△ABC 的面积为(1)求;(2)若求△ABC 的周长.20.(12 分)已知数列和满足,,,,.(Ⅰ)求与;(Ⅱ)记数列的前项和为,且,若对,恒成立,求正整数的值.21.(12 分)已知与有两个不同的交点,其横坐标分别为().(1)求实数的取值范围;(2)求证:.22.(10 分)如图,焦点在轴上的椭圆与焦点在轴上的椭圆都过点,中心都在坐标原点,且椭圆与的离心率均为.(Ⅰ)求椭圆与椭圆的标准方程;(Ⅱ)过点 M 的互相垂直的两直线分别与,交于点 A,B(点 A、B 不同于点 M),当的面积取最大值时,求两直线 MA,MB 斜率的比值.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、C【解析】根据线面平行的性质定理和判定定理判断与的关系即可得到答案.【详解】若,根据线面平行的性质定理,可得;若,根据线面平行的判定定理,可得.故选:C.【点睛】本题主要考查了线面平行的性质定理和判定定理,属于基础题.2、B【解析】根据线面垂直的判断方法对选项逐一分析,由此确...