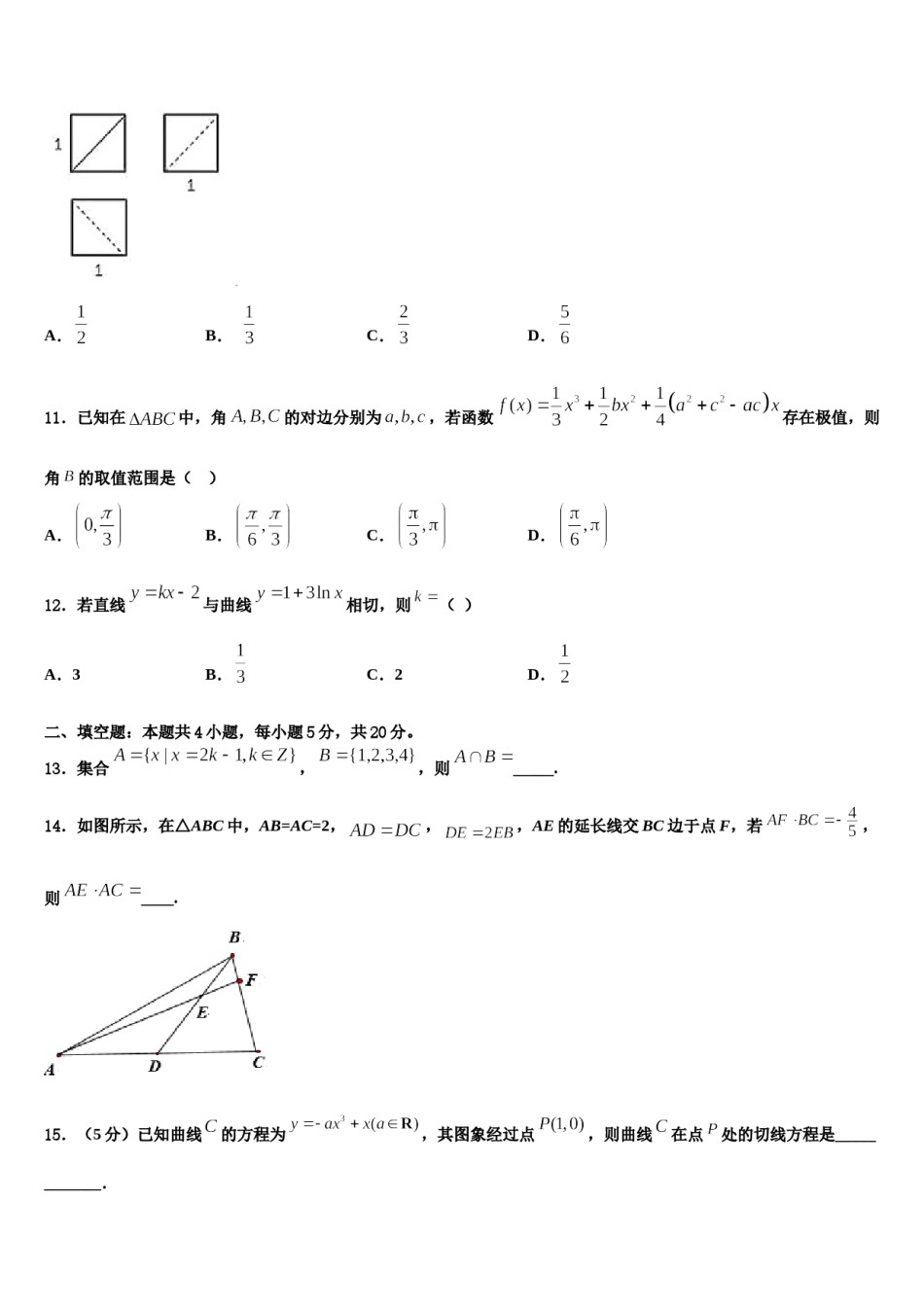
湖南省常德市石门县二中2024年高考考前提分数学仿真卷考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线的右焦点为,过原点的直线与双曲线的左、右两支分别交于两点,延长交右支于点,若,则双曲线的离心率是()A.B.C.D.2.已知抛物线的焦点为,准线为,是上一点,是直线与抛物线的一个交点,若,则()A.B.3C.D.23.已知P是双曲线渐近线上一点,,是双曲线的左、右焦点,,记,PO,的斜率为,k,,若,-2k,成等差数列,则此双曲线的离心率为()A.B.C.D.4.设全集,集合,,则()A.B.C.D.,则的取值范围是(5.函数在上单调递减,且是偶函数,若)A.(2,+∞)B.(﹣∞,1)∪(2,+∞)C.(1,2)D.(﹣∞,1)6.若函数的图象向右平移个单位长度得到函数的图象,若函数在区间上单调递增,则的最大值为().A.B.C.D.7.洛书,古称龟书,是阴阳五行术数之源,在古代传说中有神龟出于洛水,其甲壳上心有此图象,结构是戴九履一,左三右七,二四为肩,六八为足,以五居中,五方白圈皆阳数,四角黑点为阴数.如图,若从四个阴数和五个阳数中分别随机选取1个数,则其和等于11的概率是().A.B.C.D.8.做抛掷一枚骰子的试验,当出现1点或2点时,就说这次试验成功,假设骰子是质地均匀的.则在3次这样的试验中成功次数X的期望为()A.B.C.1D.29.已知双曲线的一条渐近线经过圆的圆心,则双曲线的离心率为()A.B.C.D.210.如图是正方体截去一个四棱锥后的得到的几何体的三视图,则该几何体的体积是()A.B.C.D.11.已知在中,角的对边分别为,若函数存在极值,则角的取值范围是()A.B.C.D.12.若直线与曲线相切,则()A.3B.C.2D.二、填空题:本题共4小题,每小题5分,共20分。13.集合,,则_____.14.如图所示,在△ABC中,AB=AC=2,,,AE的延长线交BC边于点F,若,则____.15.(5分)已知曲线的方程为,其图象经过点,则曲线在点处的切线方程是____________.16.记数列的前项和为,已知,且.若,则实数的取值范围为________.三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。17.(12分)已知数列满足,,数列满足.折起,使点A到达(Ⅰ)求证数列是等比数列;(Ⅱ)求数列的前项和.18.(12分)如图,在平行四边形中,,,现沿对角线将点P,点M,N分别在直线,上,且A,B,M,N四点共面.(1)求证:;(2)若平面平面,二面角平面角大小为,求直线与平面所成角的正弦值.,且19.(12分)在△ABC中,角所对的边分别为向量,向量.(1)求角的大小;(2)求的最大值.20.(12分)设为等差数列的前项和,且,.(1)求数列的通项公式;(2)若满足不等式的正整数恰有个,求正实数的取值范围.21.(12分)在平面直角坐标系xoy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为,过点的直线l的参数方程为(为参数),直线l与曲线C交于M、N两点。(1)写出直线l的普通方程和曲线C的直角坐标方程:(2)若成等比数列,求a的值。22.(10分)已知函数,.(1)讨论的单调性;(2)若存在两个极值点,,证明:.参考答案一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、D【解析】设双曲线的左焦点为,连接,,,设,则,,,和中,利用勾股定理计算得到答案.【详解】设双曲线的左焦点为,连接,,,设,则,,,,根据对称性知四边形为矩形,中:,即,解得;中:,即,故,故.故选:.【点睛】本题考查了双曲线离心率,意在考查学生的计算能力和综合应用能力.2、D【解析】根据抛物线的定义求得,由此求得的长.【详解】过作,垂足为,设与轴的交点为.根据抛物线的定...