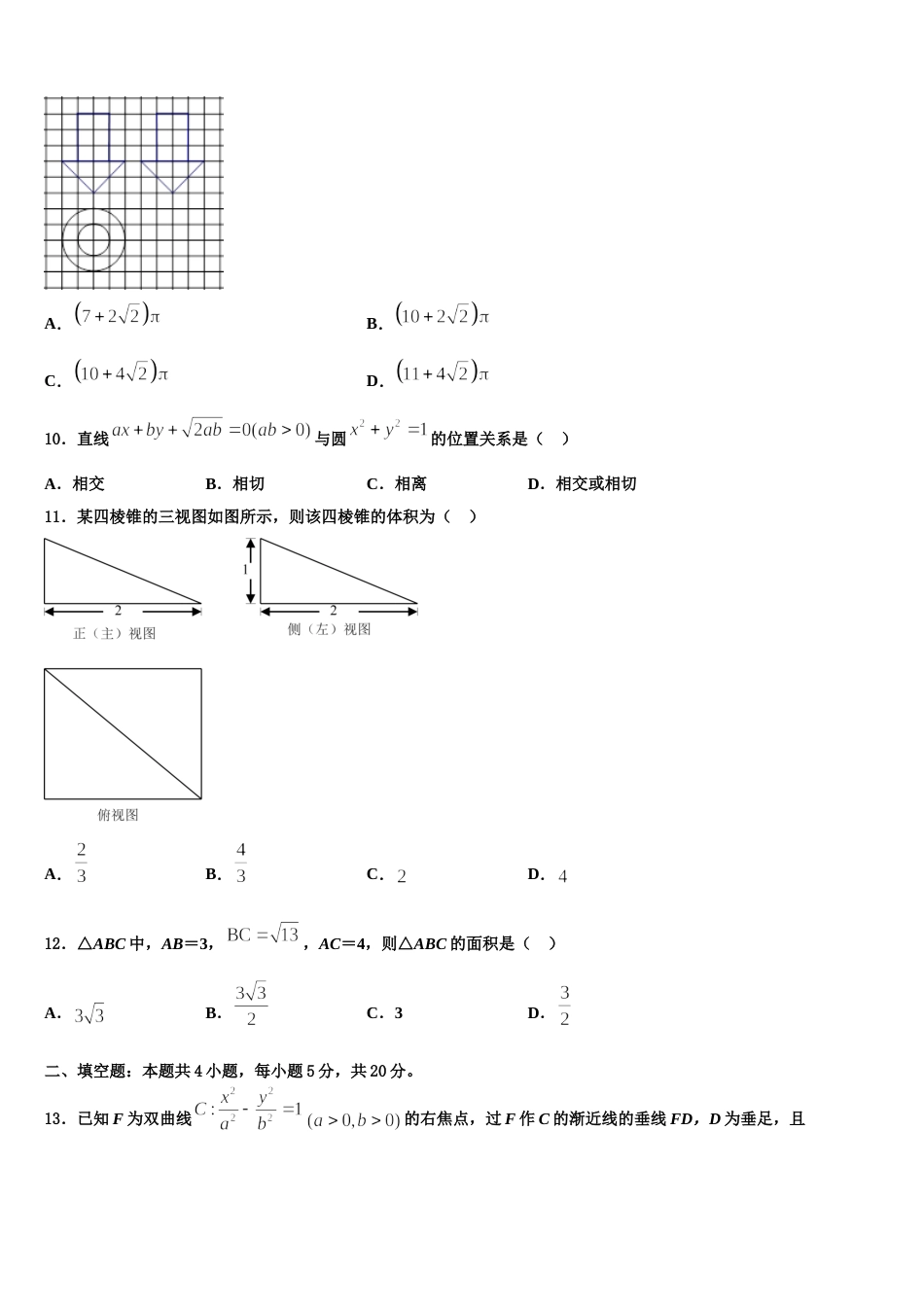
湖南省湘南联盟 2023-2024 学年高三下第一次测试数学试题注意事项1.考生要认真填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知双曲线的左右焦点分别为,,以线段为直径的圆与双曲线在第二象限的交点为,若直线与圆相切,则双曲线的渐近线方程是( )A. B.C. D.2.已知双曲线:的焦距为,焦点到双曲线的渐近线的距离为,则双曲线的渐近线方程为()A.B.C.D.3.集合的真子集的个数是( )A.B.C.D.4.木匠师傅对一个圆锥形木件进行加工后得到一个三视图如图所示的新木件,则该木件的体积( ) A.B.C.D.5.将函数的图像向右平移个单位长度,再将图像上各点的横坐标伸长到原来的 6 倍(纵坐标不变),得到函数的图像,若为奇函数,则的最小值为( )A.B.C.D.6.如图,在中,点是的中点,过点的直线分别交直线,于不同的两点,若,,则( )A.1B.C.2D.37.已知四棱锥中,平面,底面是边长为 2 的正方形,,为的中点,则异面直线与所成角的余弦值为( )A.B.C.D.8.总体由编号 01,,02,…,19,20 的 20 个个体组成.利用下面的随机数表选取 5 个个体,选取方法是随机数表第 1行的第 5 列和第 6 列数字开始由左到右依次选取两个数字,则选出来的第 5 个个体的编号为7816657208026314070243699728019832049234493582003623486969387481A.08B.07C.02D.019.陀螺是中国民间最早的娱乐工具,也称陀罗. 如图,网格纸上小正方形的边长为 ,粗线画出的是某个陀螺的三视图,则该陀螺的表面积为( )A.B.C.D.10.直线与圆的位置关系是( )A.相交B.相切C.相离D.相交或相切11.某四棱锥的三视图如图所示,则该四棱锥的体积为( )A.B.C.D.12.△ABC 中,AB=3,,AC=4,则△ABC 的面积是( )A.B.C.3D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.已知 F 为双曲线的右焦点,过 F 作 C 的渐近线的垂线 FD,D 为垂足,且(O 为坐标原点),则 C 的离心率为________.14.若 x,y 满足,且 y≥−1,则 3x+y 的最大值_____15.在平行四边形中,已知,,,若,,则____________.16.设等差数列的前项和为,若,,则______,的最大值是______.三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。17.(12 分)已知椭圆()经过点,离心率为,、、为椭圆上不同的三点,且满足,为坐标原点.(1)若直线、的斜率都存在,求证:为定值;(2)求的取值范围.18.(12 分)设函数,,其中, 为正实数.(1)若的图象总在函数的图象的下方,求实数 的取值范围;(2)设,证明:对任意,都有.19.(12 分)已知函数,其中.(Ⅰ)当时,求函数的单调区间;(Ⅱ)设,求证:;(Ⅲ)若对于恒成立,求的最大值.20.(12 分)在中,角,,的对边分别为,,,,, 且的面积为.(1)求;(2)求的周长 .21.(12 分)已知函数.(1)解不等式;(2)若函数存在零点,求的求值范围.22.(10 分)以直角坐标系的原点为极坐标系的极点,轴的正半轴为极轴.已知曲线的极坐标方程为,是上一动点,,点的轨迹为.(1)求曲线的极坐标方程,并化为直角坐标方程;(2)若点,直线 的参数方程( 为参数),直线 与曲线的交点为,当取最小值时,求直线 的普通方程.参考答案一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、B【解析】先设直线与圆相切于点,根据题意,得到,再由,根据勾股定理求出,从而可得渐近线方程.【详解】设直线与圆相切于点,因为是以圆的直径为斜边的圆内接三角形,所以,又因为圆与直线的切点为,所以,又,所以,因此,因此有,所以,因此渐近线的方程为.故选 B【点睛】本...